АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Бесконечно большие функции и их связь с бесконечно малыми функциями

Читайте также:
  1. II. Основные задачи и функции
  2. III. Предмет, метод и функции философии.
  3. IV. Двойная связь и конверсия
  4. IV. Конструкция бент-функции
  5. Ms Excel: мастер функций. Логические функции.
  6. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  7. V2: ДЕ 32 - Дифференциальное исчисление функции одной переменной. Производная
  8. V2: ДЕ 35 - Дифференциальное исчисление функции одной переменной. Производные высший порядков
  9. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  10. V2: Функции исторической науки
  11. VIII. ФУНКЦИИ НАУЧНОГО ИССЛЕДОВАНИЯ
  12. XVIII. ПРОЦЕДУРЫ И ФУНКЦИИ

Теорема о связи между бесконечно большой и бесконечно малой функциями:

Если функция - функция бесконечно малая (), то функция есть бесконечно большая функция и наоборот.

 

Доказательство:

Пусть - бесконечно малая функция при 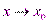, т.е. . Тогда для любого числа существует такое число 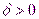, что для всех , удовлетворяющих неравенству , выполняется неравенство , т.е. , т.е. , где . А из этого следует, что функция - бесконечно большая.

 

 

9. Основные эквивалентности бесконечно малых функций.

Б.м. функции и называются эквивалентными или равносильными б.м. одного порядка при , если

Обозначают: при .

Таблица эквивалентных б.м. функций при

 

10. Непрерывность функции в точке. Непрерывность основных элементарных функций.

Функция 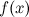называется непрерывной в точке , если:

1. функция 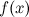определена в точке и ее окрестности;

2. существует конечный предел функции 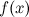в точке ;

3. это предел равен значению функции в точке , т.е.

?

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)