АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определение монотонной функции. Теорема Вейерштрасса о пределе монотонной функции. Теорема о множестве значений функции монотонной и непрерывной на отрезке

Читайте также:
  1. A) эффективное распределение ресурсов
  2. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  3. Access. Базы данных. Определение ключей и составление запросов.
  4. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  5. I. Открытые способы определения поставщика.
  6. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  7. II. Основные задачи и функции
  8. II. РАСПРЕДЕЛЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ В ОРГАНИЗМЕ. БИОЛОГИЧЕСКИЕ БАРЬЕРЫ. ДЕПОНИРОВАНИЕ
  9. II. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
  10. III. Используемые определения и обозначения
  11. III. Определение оптимального уровня денежных средств.
  12. III. Предмет, метод и функции философии.

(?) Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное[1]. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Определения:

Пусть дана функция Тогда

· функция 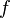называется возраста́ющей на , если

.

· функция 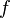называется стро́го возраста́ющей на , если

.

· функция 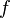называется убыва́ющей на , если

.

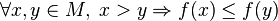· функция 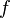называется стро́го убыва́ющей на , если

.

(?) –

(?) –


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)