АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Доказательство. Предположим, что непрерывна, но неограниченна:

Читайте также:
  1. Глава 4. Социальное доказательство.

Предположим, что непрерывна, но неограниченна: .

По лемме Больцано-Вейерштрасса, из последовательности можно извлечь частичную последовательность , сходящуюся к пределу :

. По теореме о предельном переходе в неравенстве . Так как

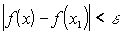, . Мы пришли к противоречию.

То есть - ограничена. .

Теорема 13.2 (Вторая теорема Вейерштрасса).

Если функция непрерывна на отрезке , то она достигает свои точные верхнюю и нижнюю грани.

Эта теорема означает, что достигаемые sup и inf означают соответственно max и min функции.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)