Угол между прямыми на плоскости

Определение. Если заданы две прямые y = k₁x + b₁, y = k₂x + b₂, то острый угол между этими прямыми будет определяться как

Две прямые параллельны, если k₁ = k₂.

Две прямые перпендикулярны, если k₁ = -1/k₂.

Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА, В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то можно найти угол. Точнее, косинус угла по формуле:

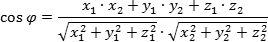
19. Плоскость в пространстве. Различные виды уравнения плоскости. Взаимное расположение плоскостей. Расстояние от точки до плоскости.
В декартовых координатах каждая плоскость определяется уравнением первой степени, и каждое уравнение первой степени определяет плоскость. Всякий вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение A(X – Xo) + B(Y – Yo) + C(Z – Zo) = 0 – 1) определяет плоскость, проходящую через точку Мо (Xo; Yo; Zo) и имеющую нормальный вектор n
= {
A
;
B
;
C
}. Раскрывая в уравнении 1) скобки и обозначая число – AXo – BYo – CZo буквой D, представим его в виде: AX + BY + CZ + D = 0. Это уравнение называется общим уравнением плоскости. Различные виды уравнения плоскости. Пусть в пространстве заданы три различные точки М1(X1; Y1; Z1) M2(X2; Y2; Z2) M3(X3; Y3; Z3). Через эти три точки можно провести плоскость единственным образом. Рассмотрим точку M(X; Y; Z) лежащую в этой плоскости, тогда выполняется условие - 1). Если условие 1) не выполняется, то точка М не лежит в этой плоскости, поэтому 1) называется уравнением плоскости проходящей через три заданные точки записанная в форме определителя. Раскроем определитель по элементам первой строки и обозначим коэффициенты, стоящие перед X,A; перед Y, B; перед Z, C, то тогда получим уравнение плоскости в виде AX + BY + CZ + D =0 – 2) – общее уравнение плоскости. Предположим, что 2) D ¹ 0 и рассмотрим плоскость, заданную уравнением AX + BY + CZ = 0 – 3). Очевидно, что система линейных уравнений, состоящая из равенств 2) и 3) не имеет решений. Это означает, что плоскости 2) и 3) не пересекаются. Следовательно, плоскость 3) êê
2). Рассмотрим производную точку М лежащую в плоскости 3), когда вектор ОМ целиком лежит в этой плоскости вектор ОМ (X; Y: Z), поэтому 3) можно рассматривать как равное нулю, скалярного произведения векторов ОМ и N (A; B; C).Тогда из 3) следует, что вектор N перпендикулярный плоскости 3). Поэтому вектор М называется нормальным вектором плоскости, т. к. 2) êê
3), то N ^ к этой плоскости, поэтому N называется нормальным вектором и для плоскости 2). 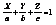- Уравнение плоскости отрезка.
Взаимное расположение плоскостей. 1) A1X + B1Y + C1Z + D1 = 0 2) A2X + B2Y + C2Z + D2 = 0. 1. Пусть плоскости 1 и 2 пересекаются. В этом случае имеются точки, принадлежащие одновременно плоскостям 1и 2. Поэтому система линейных уравнений, составленная из 1и 2 имеет по крайней мере, одно решение. Для этого необходимо и достаточно выполнения условия: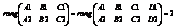
2. Если плоскость 1 параллельна 2, то это означает, что с.л.у. составленная из 1и2 не имеет решений. Для этого необходимо и достаточно выполнения условия: 3. Пусть плоскость 1и2 совпадают. .
Расстояние от точки до плоскости. Пусть точка М* - какая угодно точка пространства, d – расстояние от нее до данной плоскости. Отклонением d точки М* от данной плоскости называется число +d, если точка М* и начало координат лежат по разные стороны от данной плоскости, и число –d, если они расположены по одну сторону от данной плоскости. Если даны координаты X*, Y*,Z* точки М* и нормальное уравнение плоскости X cosa + Y cosb + Z cosg - p = 0, то отклонение d точки М* от этой плоскости может быть вычислено по формуле d = X* cosa + Y* cosb + Z* cosg - p. Очевидно d = 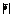. Общее уравнение плоскости Ax + By + Cz + D = 0, приводится к нормальному виду умножением на нормирующий множитель, определяемый 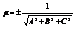. Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.

20. Прямая в пространстве. Взаимное расположение прямых и плоскостей.
Рассмотрим в пространстве две точки М1(X1; Y1; Z1) и M2(X2; Y2; Z2) можно провести единственную прямую. Пусть М(X; Y; Z) лежит на этой прямой, тогда векторы М1М2 и М1М каллинеарны М1М2(X2 – X1; Y2 –Y1; Z2 –Z1); M1M(X –X1; Y –Y1; Z – Z1). Из условия координат следует 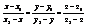- 1).1) – уравнение прямой в пространстве проходящей через две заданные точки. X2 – X1 = k Y2 –Y1 = l Z2 – Z1 = m A(k; l; m) êêпрямой проходящей через М1 и М2. - 2) уравнение прямой проходящей через заданную точку М1 с заданным направляющим вектором.
Взаимное расположение прямых и плоскостей. Пусть дана плоскость Ax + By + Cz + D = 0 - 3). Пусть дана прямая - 4). A(l; m; n)– направляющий вектор для прямой. Тогда A * n = êA ê* ên êsina. sina = = 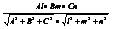- 5). Из 5) следует, что прямая 4) êê
3), тогда угол a = 0 следует Al + Bm + Cn = 0 – условие параллельности прямой плоскости. Если 4) ^
3), то a =90. - условие перпендикулярности прямой и плоскости.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость. в качестве угла между прямой и плоскостью мы выбираем острый угол. Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю. Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°. Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.признак перпендикулярности прямой и плоскости:Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

21. Кривые второго порядка. Эллипс. Гипербола. Парабола.
Общее у-е кривых второго порядка:
После изменения начала координат и переноса начала координат в новую т. или поворта координатных осей, кривые второго порядка могут быть преобразованы к более простому (каноническому) виду. В результате преобразований у-е может описывать следующие линии: эллипс; гиперболу; параболу; пару êêпрямых; пара пересекающихся прямых; точка.
Эллипс.
Эллипсом называют геометрическое место точек на плоскости, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная и большая чем расстояние между фокусами.
Пусть задан эллипс F₁ и F₂ – фокусы эллипса, выберем систему координат следующим образом, ось абсцисс проведём через фокусы, начало координат выберем между фокусами. F₁(c;0), F₂(-c,0), C>0.

Пусть т. М лежит на эллипсе êMF₁ê+êMF₂ê=const =2a>2c Þ a>c , , r₁ и r₂ –фокальные радиусы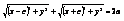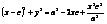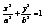. , , , , , , , , , , , , , - каноническое у-е эллипса.
Из канонического у-ия следует, что вместе с т. М лежащей на эллипсе, точки М₁(х;-у), М₂(-х;у), М₃(-х;-у) так же лежат на эллипсе, таким образом эллипс симметричен оси абсцисс и оси ординат. - вершины.

Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2 а и 2 b (2 a >2 b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2) Весь эллипс содержится внутри прямоугольника

3) Эксцентриситет эллипса e < 1.

Действительно,

4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е, а е <1, следовательно, а/е>a, а весь эллипс лежит в прямоугольнике )

5) Отношение расстояния r_i от точки эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Гиперболой называют геометрическое место точек на плоскости, модуль разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная и меньшая чем расстояние между фокусами.
Пусть дана гипербола, F₁ и F₂ – фокусы гиперболы, выберем систему координат следующим образом, ось абсцисс проведём через фокусы, начало координат выберем между фокусами. F₁(c;0), F₂(-c,0)

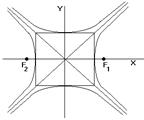
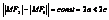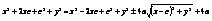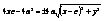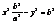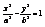, , , , , , , , , , , , , - каноническое у-е гиперболы.

Из канонического у-ия гиперболы получим , , ассимптоту гиперболы можно найти по формуле

Свойства гиперболы:

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями

и .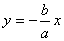

3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением

,

для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5) Отношение расстояния r_i от точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Параболой называют геометрическое место точек на плоскости, расстояние от которых до фиксированной точки, называемой фокусам, равно расстоянию до фиксированной прямой, называемой директрисой.
Выберем систему координат следующим образом, ось абсцисс проведём через фокус ^ директрисе, начало координат выберем посередине между фокусом и директрисой.

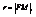тогда из определения - экцентрисситет.

Свойства параболы:

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

23. Действительные числа. Числовая последовательность. Основные понятия. Примеры.
действительные числа - все положительные, отрицательные и нуль. Пусть определено правило по которому каждому натуральному числу ставится в соответствии некоторое соответственное число, тогда говорят, что задана числовая последовательность. Мы будем рассматривать аналитический способ, в этом случае числовая последовательность задаётся с помощью математических выражений. .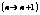
Числа которые ставятся в соответствие натуральным числам, называются элементами последовательности. .
Числовая последовательность может быть задана рекуррентным способом, в этом случае каждый элемент числовой последовательности определяется при помощи пред идущих элементов.
Числовая последовательность называется монотонно возрастающей, если каждый следующий элемент больше предыдущего.
Числовая последовательность называется монотонно убывающей, если каждый следующий элемент меньше предыдущего.
Числовая последовательность называется неубывающей, если выполняется условие
Числовая последовательность называется неубывающей, если выполняется условие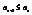
Числовая последовательность называется стационарной, если .
Числовая последовательность называется ограниченной, если можно указать такое число А, что для всех n выполняется условие
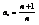- убывающая ограниченная, - ограниченная.
Пусть задана числовая последовательность, изобразим элементы этой последовательности в виде точек на числовой оси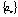

тогда монотонное возрастание ч.п. означает, что каждая следующая тока расположена правее предыдущей.
Монотонное убывание ч.п. означает, что каждая следующая тока расположена левее предыдущей.
Очевидно, что числовая последовательность , будет ограниченной тогда и только тогда, когда можно указать отрезок , такой, что " ,

24. Сходящиеся последовательности. Свойства сходящихся последовательностей.

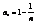
Ни для одного значения n для данной числовой последовательности не может выполнятся условие , действительно, если это условие выполнимо для данного ,
Элементы данной числовой последовательности могут сколь угодно близко располагаться около 1. , значит расстояние от точек соответствующее элементам , до точки 1 равно , поэтому какое бы не было положительное число d не было задано, всегда будет выполнятся условие , d=0,01, , n>100.
e - окрестностью числа А называется множество чисел 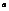удовлетворяющих неравенству 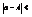e - интервал (А-e,А+e)

Пусть дана числовая последовательность . А – называется пределом числовой последовательности, если для любого сколь угодно малого числа e можно указать такй номер N, что все эти элементы числовой последовательности , будут попадать в e окрестности числа А при , , .
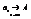Последовательность для которой существует предел, называется сходящейся.
Если число А является пределом числовой последовательности А_n, то это означает, что все элементы числовой последовательности попадают в сколь угодно малую окрестность числа А, начиная с некоторого номера.
Теорема 1: всякая сходящая числовая последовательность имеет единственный предел.
Теорема 2: всякая сходящая числовая последовательность ограничена.
Теорема 3: пусть даны три числовые последовательности, , предположим, что " n .

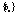Пусть последов. и являются сходящими, причём , тогда последовательность также является сходящейся и , теорема о двух милиционерах.

Выберем произвольное положительное число e, "e найдём N₁ и N₂, такие чтобы выполнялись Þ неравенства:
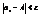, (1)

, (2)
N – max из (N₁, N₂), тогда "n>N одновременно выполняются неравенства:
А-e<a_n<A+e (3)
А-e<c_n<A+e (4)
Поэтому "n>N выполняются неравенство:
А-e<a_n <A+e, А-e<b_n<A+e, , таким образом является сходящейся и имеет .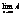
Теорема 4: всякая монотонно возрастающая ограниченная числовая последовательность является сходящейся.
Всякая монотонно убывающая ограниченная числовая последовательность является сходящейся.
Арифметические св-ва сходящихся последовательностей.
, .
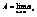Теоремы:
1)
2)
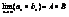
3) А¹0,

Поиск по сайту: