Условие монотонности и стационарности функции на интервале

Теорема 1. Для того чтобы дифференцируемая на интервале (a;b) функция возрастала (убывала) на этом интервале достаточно, чтобы производная была положительной (отрицательной) всюду на этом интервале.

Доказательство. Рассмотрим случай, когда 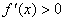. Пусть x1 и x2 - любые две точки интервала (a;b), удовлетворяющие условию . На отрезке функция дифференцируема, а, следовательно, непрерывна. Поэтому к ней можно применить формулу Лагранжа:

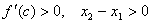, где . По условию . Поэтому или , т.е. функция возрастает на интервале (a;b). Случай, когда , рассматривается аналогично.Теорема доказана.

Из последней теоремы следует, что отличие от нуля производной является достаточным условием строгой монотонности функции. Однако это условие не является необходимым. Так, например, функция возрастает на любом интервале действительной оси, но при x=0 производная этой функции обращается в нуль (рис. 6). Следующая теорема устанавливает необходимое и достаточное условие монотонности функции.Теорема 2. Для того чтобы дифференцируемая на интервале (a;b) функция не убывала (не возрастала) на этом интервале, необходимо и достаточно, чтобы производная этой функции была неотрицательной (неположительной) всюду на этом интервале.

Доказательство. 1) Докажем достаточность. Пусть 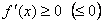. Рассмотрим любые две точки x1 и x2 интервала (a;b), удовлетворяющие условию . Повторяя рассуждения из доказательства предыдущей теоремы, получим: , где . Так как по условию , то , или , т.е. функция не убывает (не возрастает) на интервале (a;b).

2) Докажем необходимость. Пусть функция дифференцируема и не убывает (не возрастает) на интервале (a;b). Так как эта функция не убывает (не возрастает) на

интервале (a;b), то она не может убывать (возрастать) ни в одной точке интервала (a;b). Поэтому, как следует из теоремы 16.1, производная ни в одной точке интервала (a;b) не может быть отрицательной (положительной).Теорема доказана.

Стационарность - наибольшее и наименьшее значение функции. Находится через первую производную приравненной к нулю.

46. Понятие локального экстремума. Необходимое и достаточное условие существования экстремума.
Функция f(x) имеет максимум (минимум) в точке x=a, если значение f(a) больше (меньше) всех соседних значений. Максимум и минимум объединяются наименованием экстремум.
Необходимое условие максимума и минимума:
Если функция f(x) имеет экстремум в точке x=a, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует.
Первое достаточное условие экстремума:
Если в достаточной близости от точки x=a производная f’(x) положительна слева от a и отрицательна справа от a, то в самой точке x=a функция f(x) имеет максимум при условии, что функция f(x) здесь непрерывна.
Второе достаточное условие экстремума:
Пусть в точке x=a первая производная f’(x) обращается в нуль; если при этом вторая производная f’’(a) отрицательна, то функция f(x) имеет в точке x=a максимум, если положительна, то – минимум.
47. Выпуклые функции. Условия выпуклости.
Кривая обращена выпуклостью вверх на интервале (a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале. Кривая обращена выпуклостью вниз на интервале (b, c), если все точки кривой лежат выше любой ее касательной на этом интервале.

Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f’’(x)<0, то кривая y=f(x) на этом интервале обращена выпуклостью вверх (кривая выпукла).

Теорема 1'. Если во всех точках интервала (b, c) вторая производная функции f(x) положительна, т.е. f’’(x)>0, то кривая y=f(x) на этом интервале обращена выпуклостью вниз (кривая вогнута).

Теорема 2. Пусть кривая определяется уравнением y=f(x). Если f’’(a)=0 или f’’(a) не существует и при переходе через значение x=a производная f’’(x) меняет знак, то точка кривой с абсциссой x=a есть точка перегиба.

48.Формула Тейлора. Формулы Тейлора для элементарных функций. Примеры.
Теорема: Если функция f(x) обладает в замкнутом промежутке (a, b) производными до (n+1)-го порядка включительно, то

где x - некоторое число, лежащее между a и b.
Последнее слагаемое в формуле, называемое остаточным членом в форме Лагранжа, дает точное выражение разности R_n между f(b) и выражением
(многочлен Тейлора):
Формула Тейлора устанавливает что уравнение, в котором за неизвестное принимается x, имеет, по меньшей мере, одно решение, лежащее между a и b.
Пример: Пусть f(x)=e^x. Все производные этой функции равны e^x. Нам известно значение e^x в точке х=0 (именно e⁰=1). Эту точку мы примем за начальную. В многочлене Тейлора надо положить: a=0, f(a)=f’(a)=…=f⁽ⁿ⁾(a)=1, и он принимает такой вид(5):
Заменив значение e^x значением многочлена (5), мы допустим некоторую ошибку R_n; она равна
Число x лежит где-то между нулём и x (оно зависит и от x и от n). Значит, e^x лежит между e⁰=1 и e^x. Этого достаточно, чтобы оценить ошибку.
34. Точка разрыва ф-ии. Односторонние пределы.
Пусть задана ф-я y=f(x), х₀ÎХ, для данной ф-ии можно определить односторонний предел.
Число А называют правосторонним пределом ф-ии y=f(x), если " числовой последовательности сходящейся к точке х₀ и такокй, что x_n>x₀. .

Аналогичным образом определяется левосторонний предел.
Нарушение условий непрерывности для ф-ии y=f(x), может происходить как в отдельных точках, так и в точках образующих одну или несколько линий.

Поиск по сайту: