Волновое уравнение для электромагнитных волн

Как уже отмечалось в предыдущей части курса, ротор (rot) и дивергенция (div) – это некоторые операции дифференцирования, производимые по определенным правилам над векторами. Ниже мы познакомимся с ними поближе.

Возьмем ротор от обеих частей уравнения

При этом воспользуемся доказываемой в курсе математики формулой:

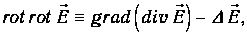
где D – введенный выше лапласиан. Первое слагаемое в правой части равно нулю в силу другого уравнения Максвелла:

Получаем в итоге:

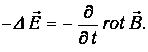
(3.93)

Выразим rot B через электрическое поле с помощью уравнения Максвелла:

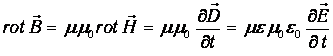
(3.94)

и используем это выражение в правой части (3.93). В результате приходим к уравнению:

(3.95)

Учитывая связь

и вводя показатель преломления среды

запишем уравнение для вектора напряженности электрического поля в виде:

(3.96)

Сравнивая с (3.69), убеждаемся, что мы получили волновое уравнение, где v – фазовая скорость света в среде:

(3.97)

Взяв ротор от обеих частей уравнения Максвелла

и действуя аналогичным образом, придем к волновому уравнению для магнитного поля:

(3.98)

Полученные волновые уравнения для Е и Н означают, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна

В отсутствие среды (при e=m=1) скорость электромагнитных волн совпадает со скоростью света в вакууме.

Поиск по сайту: