Анализ решений

Итак, в обоих рассмотренных случаях дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:

(1.67)

где x – переменная (смещение, заряд, ток), описывающая колебания, b – коэффициент затухания, a w₀ – циклическая частота свободных (собственных) незатухающих колебаний (то есть при b=0, при отсутствии потерь энергии). Сведем новую задачу к предыдущей. Для этого вместо переменной xопределим новую переменную X, связанную с x соотношением:

(1.68)

Дифференцируя функцию x(t), получаем:

(1.69)

Подставляем эти выражения в (1.67):

(1.70)

Выражение в квадратных скобках должно быть равно нулю. Замечаем, что в этом выражении сокращаются члены с первой производной dX/dt Получаем в итоге дифференциальное уравнение для функции X(t):

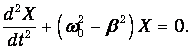
(1.71)

Здесь возможны два случая. Пусть сначала b<w₀. Тогда можно ввести параметр

так что уравнение (1.71) примет вид:

Но это – стандартное уравнение гармонических колебаний, общее решение которого мы знаем:

Значит, мы нашли общее решение уравнения затухающих колебаний (1.67):

(1.72)

Во многих системах коэффициент затухания мал по сравнению с собственной частотой колебаний: b<<w₀. Тогда движение системы можно рассматривать как почти гармоническое колебание с частотой w₀ и с амплитудой, изменяющейся по закону (рис. 1.22)

Рис. 1.22. Свободные затухающие колебания

Коэффициент затухания b определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.

Период затухающих колебаний равен:

(1.73)

Пусть первое наибольшее отклонение достигается в момент времени t=t*. Последующие наибольшие отклонения (A', A'', A''' и т.д. – см. рис. 1.20) образуют геометрическую прогрессию:

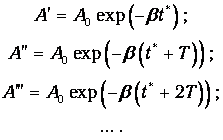
(1.74)

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:

(1.75)

Это соотношение называется декрементом затухания. Логарифм этого отношения называется логарифмическим декрементом затухания:

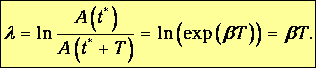
(1.76)

Определим количество колебаний, которое совершит система за время t=1/b. За это время амплитуда уменьшается в е раз, а число колебаний равно:

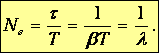
(1.77)

Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.

Для характеристики колебательной системы часто употребляется величина, называемая добротностью:

(1.78)

которая пропорциональна числу колебаний N_е, совершаемых системой за то время t, за которое амплитуда колебаний уменьшается в е раз. Например, для электромагнитного контура при b<<w₀ находим:

(1.79)

Мы видели, что полная энергия в колеблющейся системе пропорциональна квадрату амплитуды. При малом затухании (b<<w₀) имеем:

(1.80)

где E₀– значение полной энергии колеблющейся системы в начальный момент времени. Можно определить убыль энергии за период Т:

(1.81)

Следовательно,

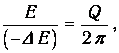
(1.82)

то есть при слабом затухании добротность, с точностью до множителя 1/(2p), равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.

При увеличении затухания частота колебаний

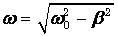
стремится к нулю, а период колебаний растет. В предельном случае

период обращается в бесконечность, то есть движение перестает быть периодическим. Соответствующий математический анализ показывает, что при b > w₀ движение носит апериодический характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.

Экспериментальное изучение затухающих колебаний математического маятника показано на рис. 1.23.

Рис. 1.23. Экспериментальное изучение затухающих колебаний математического маятника

Исследование с помощью модели зависимости амплитуды затухающих колебаний от коэффициента затухания показано на рис. 1.24.

Рис. 1.24. Исследование зависимости амплитуды затухающих колебаний от коэффициента затухания системы

Поиск по сайту: