Колебания в идеальном газе

Рассмотрим колебания в газе, происходящие вдоль одной оси х. В отличие от струны частицы газа смещаются здесь в продольном направлении, и величины смещения мы будем обозначать тем же символом u(x,t).

Рассмотрим элементарный объем газа V₀, ограниченный сечениями 1 и 2, находящимися в точке с координатами х и х+Dх (рис. 3.2). Масса газа в объеме равна Dm=r?SDx, где r – плотность газа, a S – площадь поперечного сечения. В стационарном состоянии давление газа равно р₀.

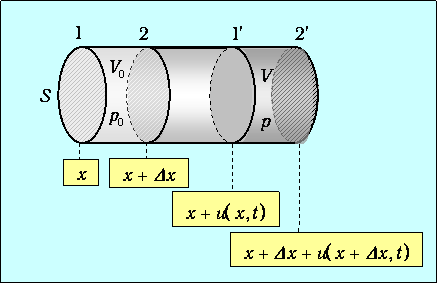
Рис. 3.2. Колебания в газе

При колебаниях выделенный объем смещается в новое положение между сечениями 1' и 2' с координатами

и

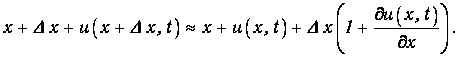
Объем газа в новом положении становится равным

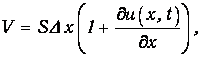
а давление в нем – р. Найдем это давление.

Колебательные процессы в газах происходят достаточно быстро, так что можно считать, что элементарный объем не успевает обмениваться теплотой с соседними объемами. Значит, процесс можно считать адиабатным. Записываем уравнение этого процесса:

или

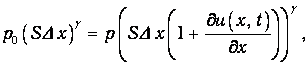
откуда

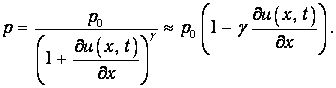
(3.4)

Здесь g – показатель адиабаты, зависящий от вида газа. Мы использовали также малость производной

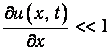
для разложения в ряд:

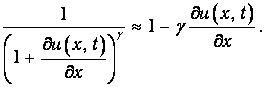
Составим теперь уравнение движения элементарного объема. Его ускорение равно

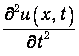
Сила, действующая на объем, определяется разностью давлений в сечениях 1' и 2':

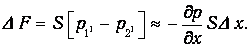
(3.5)

Подставляя сюда выражение для давления р находим:

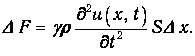
(3.6)

Записываем теперь уравнение второго закона Ньютона

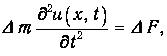
или

(3.7)

Это уравнение можно представить в виде:

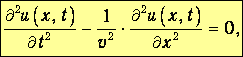
(3.8)

где

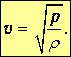
(3.9)

Величина v имеет размерность скорости. Уравнение колебаний газа совпало с уравнением колебаний струны (3.2), хотя они описывают процессы в совершенно различных физических системах.

Поиск по сайту: