Решение волнового уравнения

Уравнение типа (3.2), описывающее колебания различных упругих сред, называется волновым уравнением. Запишем его формально в виде:

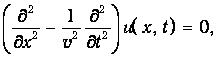
(3.16)

или

(3.16')

Введем теперь вместо (x, t) новые переменные:

(3.17)

Производные по новым переменным выражаются по стандартным правилам дифференцирования сложной функции:

Отсюда следует, что уравнение (3.16) в новых переменных записывается в виде:

(3.18)

Поскольку производная по c равна нулю, то

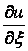
не зависит от этой переменной и, следовательно, является некоторой функцией w только от переменной x:

(3.19)

Интегрируем теперь это уравнение:

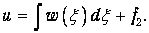
(3.20)

Первое слагаемое в правой части является только функцией переменной x, которую мы обозначим как f₁(x). Второе слагаемое – постоянная интегрирования. Она не зависит от x, являясь, стало быть, функцией только переменной c:

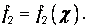
Мы получили, что решение волнового уравнения имеет вид:

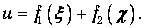
Подставляя сюда выражения (3.17), мы возвращаемся к прежним переменным (x, t):

(3.21)

Функции f₁ и f₂– совершенно произвольны и должны быть определены из начальных условий.

Обсудим физический смысл полученных решений. Ограничимся сначала первым слагаемым. Пусть

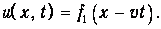
В момент времени t=0 функция f₁(x) задает распределение смещений (профиль струны, деформацию твердого тела, распределение давления или частиц в газе и т.д.):

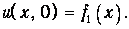
Предположим, например, что это распределение имеет максимум в точке х=x₀ (рис. 3.6).

Рис. 3.6. Движение волнового пакета f₁(x – vt)

Такое распределение называют обычно волновым пакетом. В момент t волновой пакет не изменит свою форму, но сдвинется вправо на расстояние vt, так что максимум теперь придется на точку

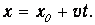
Мы видим, что начальное распределение движется вправо со скоростью v. Аналогично, второе слагаемое? f₂(x+vt) описывает движение волнового пакета налево с той же скоростью. Общее решение (3.21) является суперпозицией двух описанных.

В свою очередь, любой волновой пакет может быть представлен как суперпозиция гармонических функций. Отсюда – особая роль решений волнового уравнения вида:

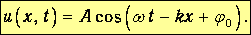
(3.22)

Это решение описывает монохроматическую волну, распространяющуюся направо со скоростью

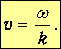
(3.23)

Действительно, выражение (3.22) можно представить в виде

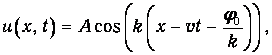
что является одной из бесчисленных возможностей конкретного воплощения функции f(x–vt) в (3.21). Величина w – это циклическая частота колебаний, а k называется волновым числом.

Пусть наблюдатель находится в точке х = x₀ и следит за колебаниями среды в этой точке. Он обнаружит, что колебательное движение происходит по закону

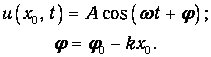
(3.24)

Наблюдатель в другой точке также обнаружит гармонические колебания с той же частотой, но с другой начальной фазой j. Чем правее точка наблюдения, тем большее запаздывание по фазе имеют там колебания. Соответственно, выражение

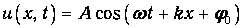
описывает монохроматическую волну, распространяющуюся налево.

Проведем теперь другой мысленный опыт: «сфотографируем» нашу волну в какой-то данный момент времени t=t₀ (в случае колеблющейся струны для этого даже не нужно изощренных приборов). На снимке мы увидим периодическую пространственную структуру:

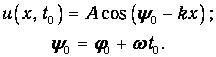
(3.25)

Эта структура имеет максимумы смещений (рис. 3.7) в точках с координатами х_п, определяемыми из условия

Рис. 3.7. Смещение точек среды в момент времени t (сплошная кривая) и t + D t (пунктирная кривая).

Период повторения l тех же смещений в пространстве есть расстояние между ближайшими максимумами:

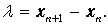
Получаем в итоге:

(3.26)

Величина l называется длиной волны.

Если «сфотографировать» волну в близкий момент времени t = t₀+Dt, то на снимке вся пространственная структура сдвинется как целое на расстояние D х = v D t. Скорость v называется фазовой скоростью волны, так как с такой скоростью движутся максимумы, минимумы и вообще все точки с данным значением фазы.

Используя (3.26) и (3.23), находим связь между характеристиками волны:

(3.27)

Здесь n=w/2p – частота колебаний в волне.

Изучение свойств бегущей волны проведем с помощью интерактивной модели (рис. 3.8).

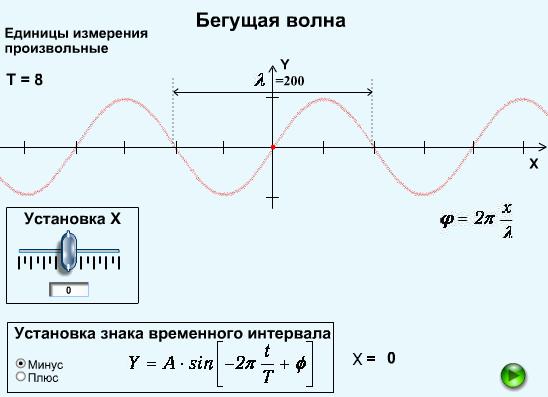
Рис. 3.8. Изучение свойств бегущей монохроматической волны

Приведем численные примеры. Волна сгущений и разрежений в газе есть продольная упругая волна. Используя уравнение Менделеева-Клапейрона для газового состояния, можно записать (3.8) в виде:

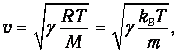
(3.28)

где М – молярная масса, т – масса молекул, а T – абсолютная температура газа. С другой стороны, среднеквадратичная скорость определяется его абсолютной температурой

откуда

(3.29)

Иными словами, скорость звука в газе по порядку величины совпадает со скоростью теплового движения молекул, будучи меньше него примерно в полтора раза. Молярная масса воздуха М =29·10^-3 кг/моль, показатель адиабаты g=1.4. Подставляя эти значения в (3.28), находим скорость звука в воздухе при комнатной температуре (T=20°С=293 К):

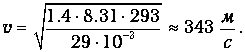
(3.30)

Человеческое ухо воспринимает частоты в диапазоне от 20 Гц до 20 кГц. Соответствующие длины волн равны:

для низких частот и

– для высоких.
Для стали модуль Юнга равен Е =20.6·10¹⁰ Н/м², модуль сдвига G=8·10¹⁰ Н/м², а плотность r=7.8·10³ кг/м³. Соответственно, получаем из (3.14), (3.15) скорости распространения продольных и поперечных колебаний в стали:

(3.31)

Наконец, для воды роль модуля Юнга играет величина, обратная сжимаемости k=0.47·10^-9 Па^-1. Плотность воды r=10³ кг/м³. Для скорости звука в воде получаем тогда:

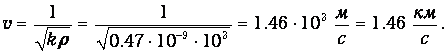
(3.32)

Звук той же частоты будет иметь в воде и воздухе разные длины волн. Так, для n=20 кГц получаем длину волны в воде:

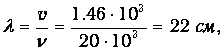
что надо сравнить с l=17 мм в воздухе.
Рассмотрим несколько примеров для оценки длины звуковой волны в различных средах.

Пример 1. Для диагностики опухолей в мягких тканях применяется ультразвук с частотой n=2 МГц. Найдем длину ультразвуковой волны в воздухе и в мягких тканях, где скорость распространения звука равна v =1.5 км/с.

Длина ультразвуковой волны в воздухе

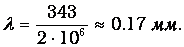
В мягких тканях длина ультразвуковой волны равна

Как мы увидим в дальнейшем, длина волны любого излучения накладывает естественный предел на размеры объектов, которые можно различить с его помощью. Данный пример показывает, что диагностика опухолей, размеры которых меньше миллиметра, с помощью ультразвука затруднительна.

Пример 2. Летучая мышь использует для ориентирования ультразвук с частотой n=100 кГц. Определим размеры препятствий, которые заведомо не будут замечены летучей мышью и ответим на тот же вопрос в отношении дельфинов, которые также используют эти частоты.

Длина волны, испускаемой летучей мышью, равна

Препятствия меньших размеров заведомо не могут быть замечены мышью с помощью испускаемой ультразвуковой волны.

Для дельфинов ответ иной из-за другой скорости распространения звука в воде. Скорость звука в воде 1.46 км/с. Тогда

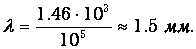
Таким образом, летучая мышь может обнаружить насекомых, а дельфин – небольших рыбок.

Пример 3. Альпинист, спускающийся с отвесной скалы, висит на веревке длиной 30 м. Страхующий его партнер подает ему сигнал, дергая веревку. Найдем, за какое время сигнал достигнет альпиниста. Масса альпиниста 80 кг, масса одного метра веревки равна 75 г.

Так как нам дана линейная плотность веревки 7.5·10^-2 кг/м и сила ее натяжения Т=тg, то по формуле (3.3) находим скорость распространения колебаний:

Отсюда определяем время прохождения сигнала:

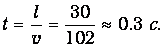
Поиск по сайту: