Сложение колебаний с одинаковыми частотами

Для простоты рассмотрим сначала случай, когда частоты складываемых колебаний одинаковы. Общие решения складываемых гармонических колебаний имеют вид:

(1.34)

где x₁, x₂ – переменные, описывающие колебания, A₁, A₂ – их амплитуды, а a₁, a₂ – начальные фазы. Результирующее колебание

удобно найти с помощью векторной диаграммы. Этот метод использует аналогию между вращением и колебательным процессом.

Возьмем общее решение (1.23) для гармонического колебания. Выберем ось 0x. Из точки 0 отложим вектор длиной A, образующий с осью 0x угол a. Если привести этот вектор во вращение с угловой скоростью w₀, то проекция конца этого вектора будет перемещаться по оси 0xот +A до –A, причем величина проекции будет изменяться по закону

(1.35)

Таким образом, проекция конца вектора на ось 0x будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени (рис. 1.12).

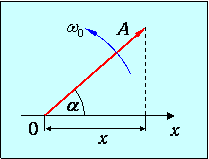
Рис. 1.12. Векторная диаграмма для общего решения (1.23)

Применим теперь эту технику к сложению колебаний (1.34). Представим оба колебания с помощью векторов А ₁ и А ₂ Возьмем их векторную сумму (рис. 1.13)

Рис. 1.13. Векторная диаграмма для сложения одинаково направленных колебаний одинаковой частоты

Проекция вектора А ₁ на ось 0x равна сумме проекций соответствующих векторов

Таким образом, вектор А представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью w₀, так что результирующее движение будет гармоническим колебанием с частотой w₀, амплитудой A и начальной фазой a. Имеем согласно теореме косинусов:

(1.36)

В частности, если фазы складываемых колебаний равны или отличаются на четное кратное p (то есть a₁-a₂=2pn), то амплитуда результирующего колебания равна сумме амплитуд

Если же складываемые колебания находятся в противофазе (то есть a₁-a₂=(2n+1)), то

Биения

В этом разделе мы рассмотрим случай сложения одинаково направленных гармонических колебаний с разными частотами. На практике особый интерес представляет случай, когда складываемые колебания мало отличаются по частоте. Как мы увидим, в результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой, называемые биениями.

Для простоты рассмотрим случай, когда амплитуды складываемых колебаний равны A, а начальные фазы обоих колебаний равны нулю. Частоты складываемых колебаний равны, соответственно, w и w+Dw. Итак,

(1.37)

Складываем эти выражения и учитываем известную формулу тригонометрии:

(1.38)

Если то в аргументе второго косинуса мы можем пренебречь сдвигом частоты:

(1.39)

Кроме того, множитель в скобках меняется медленно по сравнению с cos wt. Поэтому результирующее колебание x можно рассматривать как гармоническое колебание с частотой w, эффективная амплитуда A_эфф которого изменяется со временем по закону (1.40) (рис. 1.14):

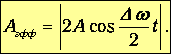
(1.40)

Рис. 1.14. Биения при сложении колебаний с близкими частотами

Частота пульсаций амплитуды (ее называют частотой биений) равна разности частот складываемых колебаний. Период биений равен

Поиск по сайту: