Гармоники

На струне, закрепленной на одном конце, могут существовать колебания любых частот. Закрепим теперь второй конец струны в точке с координатой х=l. Имеем то же решение (3.53), которое должно удовлетворять дополнительному граничному условию:

Это означает, что

На струне длиной l, закрепленной на обоих концах, могут существовать только стоячие волны с волновыми векторами

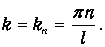
Соответственно, длины волн будут

Иными словами, на длине струны должно укладываться целое число полуволн. Следовательно, закрепленная с обоих концов струна может колебаться только с определенными частотами:

(3.58)

Мы использовали здесь уравнение (3.2) для скорости волн на натянутой струне.

Из (3.58) видно, что частота колебаний повышается при:

· уменьшении длины струны;

· уменьшении ее толщины (линейной плотности);

· увеличении натяжения.

Эти закономерности известны каждому, кто держал в руках хотя бы гитару. Колебания с низшей частотой (n=1) называются основной (первой) гармоникой, с последующими частотами – высшими (второй, третьей и т.п.) гармониками.

Аналогичные граничные условия существуют и для колебаний воздуха в трубах духовых музыкальных инструментов. Соответственно, в их сигналах также присутствуют только вполне определенные частоты. Рассмотрим, например, органную трубу длиной l. Волна давления в ней также может быть описана уравнением вида (3.53):

Если труба открыта с обеих сторон, то давление на концах равно стационарному (атмосферному) и Dр=0 в точках х =0, l. Отсюда получаем те же условия для волновых чисел

длин волн

и частот

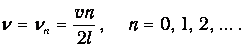
Если же труба открыта в точке х=0 и закрыта на другом конце ( х=l), то на закрытом конце смещение частиц равно нулю, а давление достигает максимума или минимума:

Отсюда следуют несколько иные соотношения:



Первая гармоника для такой трубы возбуждается на частоте

что в два раза меньше частоты

первой гармоники полностью открытой трубы.

Пример 3. Нейлоновая гитарная струна имеет линейную плотность массы 7.2 г/м и натянута с силой 150 Н. Длина струны 90 см. Определим, каковы четыре низшие частоты, извлекаемые на такой струне?

Скорость волны на струне равна

Наибольшая длина стоячей волны в струне равна l=2l=1.8 м. Отсюда находим самую низкую частоту:

(Эта частота соответствует ноте «фа» большой октавы.)
Следующие частоты являются целыми кратными n₁ :

Отсюда следует: n₁=2·87.3=174.6 Гц («фа» малой октавы), n₃=3·87.3=261.9 Гц («до» первой октавы) и n₁ = 4·87.3=349.2 Гц («фа» первой октавы).

Пример 4. Струна звучит на ноте «до» первой октавы. Максимальное отклонение точек струны от положения равновесия равно и_тах=2 мм. Найдем максимальную скорость и ускорение точек струны.

Закон колебания струны имеет вид (ср. (3.53)):

(3.59)

откуда находим скорость и ускорение точек струны:

(3.60)

По условию w=2pn₃=1 645.6 Гц (см. пример 3.). Максимальные значения скорости и ускорения равны:

Поиск по сайту: