 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Энергия и импульс электромагнитного поля
Объемная плотность энергии w электромагнитной волны складывается из объемных плотностей wэл электрического и wM магнитного полей:

| (3.123) |
Учитывая связь векторов Е и Н, получим, что плотности энергии электрического и магнитного полей в каждый момент времени одинаковы, то есть wэл=wM. Следовательно, w можно представить в виде:

| (3.124) |
Если умножить плотность энергии w на скорость электромагнитной волны в среде

то получим модуль плотности потока энергии:

| (3.125) |
Так как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора

совпадает с направлением распространения волны, то есть с направлением переноса энергии, а модуль этого вектора равен ЕН. Следовательно, вектор плотности потока электромагнитной энергии, называемый вектором Умова-Пойтинга, имеет вид:

| (3.126) |
Как и для упругих волн, интенсивность электромагнитной волны – это среднее значение плотности потока энергии:

С учетом (3.107) между Е 0 и Н 0 получаем

| (3.127) |
Как и в упругой (звуковой) волне,
| интенсивность пропорциональна квадрату амплитуды колебаний. |
Пример 2. Интенсивность солнечного излучения, падающего на Землю, составляет I=1.4 кВт/м2 (солнечная постоянная). Найдем среднюю амплитуду колебаний E0 вектора электрической напряженности в солнечном излучении. Вычислим амплитуды колебаний напряженности магнитного поля H0 и вектора магнитной индукции B0 в волне.
Ответ находим сразу из уравнений (3.127), где полагаем e=m=1:

Электромагнитные волны поглощаются или отражаются телами, следовательно, они должны оказывать на тела давление. Рассмотрим плоскую электромагнитную волну, падающую нормально на плоскую проводящую поверхность. В этом случае электрическое поле волны возбуждает в теле ток, пропорциональный Е. Магнитное поле волны по закону Ампера будет действовать на ток с силой, направление которой совпадает с направлением распространения волны. В 1899 г. в исключительно тонких экспериментах П.И. Лебедев доказал существование светового давления. Можно показать, что волна, несущая энергию W, обладает и импульсом:
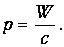
| (3.128) |
Пусть электромагнитная волна падает в вакууме по нормали на площадь А и полностью поглощается ею. Предположим, что за время Dt площадка получила от волны энергию DW. Тогда переданный площадке импульс равен

На площадку действует со стороны волны сила

Давление Р, оказываемое волной, равно

Если средняя плотность энергии в волне равна <w>, то на площадь А за время Dt попадет энергия из объема АсDt и

Отсюда находим давление электромагнитной волны (света):

| (3.129) |
Если площадка идеально отражает всю падающую на нее энергию, то давление будет в два раза большим.
Пример 3. Найдем давление Р солнечного света на Землю. Используем значение солнечной постоянной из предыдущего примера. Искомое давление равно:

Пример 4. Найдем давление Р лазерного пучка на поглощающую мишень. Выходная мощность лазера N=4.6 Вт, диаметр пучка d=2.6 мм.
Площадь сечения пучка лазерного излучения

интенсивность излучения

Отсюда находим:

Поиск по сайту: