 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Колебания двух связанных осцилляторов
Приведем поучительный пример системы, в которой возникают биения. Рассмотрим два груза массой m, которые могут колебаться по действием двух одинаковых пружин с коэффициентами жесткости k. Пусть грузы соединены также мягкой пружиной с коэффициентом жесткости K<<k. Будем полагать длины всех пружин в нерастянутом состоянии одинаковыми и равными 2L (рис. 1.15).

Рис. 1.15. Пример связанных осцилляторов. Колебания происходят вдоль оси 0х, сила тяжести не учитывается
Тогда в положении равновесия координаты грузов равны

При колебаниях координаты равны, соответственно, x1(t), x2(t). Удлинения пружин записываются как

Мы имеем дело с системой с двумя степенями свободы. Составим уравнения движения. На первый груз действуют сила со стороны пружины k, равная

и сила со стороны пружины K, равная

На второй груз действуют аналогичные силы

и

Соответственно, уравнения движения имеют вид

| (1.42) |
Эти уравнения не слишком похожи на первый взгляд на уравнения гармонических колебаний, потому что на колебания x1 оказывают влияния колебания x2 и наоборот. Поэтому преобразуем уравнения к новым переменным, колебания которых были бы независимыми (такие переменные называют нормальными колебаниями (модами). Именно, введем новые переменные x1 иx2:

| (1.43) |
Как легко убедиться, положению равновесия соответствуют координаты

В этих переменных уравнения (1.42) принимают вид:

| (1.44) |
Складывая и вычитая эти уравнения, приходим к паре независимых уравнений для колебаний нормальных мод:

| (1.45) |
Первое уравнение описывает гармонические колебания с частотой
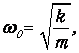
совпадающей с частотой колебаний пружинных маятников в отcутствие соединительной пружины К. Второе уравнение описывает колебания со сдвинутой частотой

Так как K<<k, имеем

| (1.46) |
Соответственно, мы получаем общее решение системы уравнений:

| (1.47) |
Общее решение для координат х1 и х2 колеблющихся точек следуют из (1.47) и (1.43):

| (1.48) |
Для примера рассмотрим случай, когда первая масса оттягивается на расстояние a от положения равновесия и отпускается с нулевой начальной скоростью, а вторая масса остается в положении равновесия:

| (1.49) |
Этому соответствуют начальные условия для нормальных мод:

| (1.50) |
Такие уравнения мы уже решали выше. Ответ будет

| (1.51) |
Подставляя найденные амплитуды и начальные фазы в (1.48), получаем решения, описывающие биения наших масс около их положений равновесия:

| (1.52) |
Графики функций x1(t), x2(t) показаны на рис. 1.16.

Рис. 1.16. Биения в системе двух связанных осцилляторов
В начальный момент времени колеблется лишь первый груз. Затем начинает колебаться второй, а амплитуда колебаний первого уменьшается. Через время t=p/Dw???первый груз останавливается, а второй колеблется с максимально возможной амплитудой. Произошла «перекачка» энергии от первого маятника ко второму. Затем процесс «перекачки» энергии идет в обратном направлении и к моменту t =2p/Dw первый маятник колеблется с максимальной амплитудой, а второй покоится.
На рис. 1.17 демонстрируются биения в системе двух связанных математических маятников.

Рис. 1.17. Биения в системе связанных маятников
Выясним теперь физический смысл нормальных мод, соответствующих чисто гармоническим колебаниям системы. Если возбуждены колебания только первой из них (x1), то A 2= 0 и, как следует из общего решения (1.48),

| (1.53) |
Иными словами, первая нормальная мода соответствует такому колебанию, когда оба груза смещаются на одинаковые расстояния от их положений равновесия, но в противоположные стороны. Скорости движения грузов также равны по величине и противоположны по направлению, так что центр масс грузов остается неподвижным. Колебания происходят под действием пружин с жесткостью k, к которым добавляется соединительная пружина с жесткостью К. Как следствие, частота таких колебаний больше частоты колебаний несвязанных осцилляторов
Возбуждение только второй (x2) нормальной моды означает, что A1=0:

| (1.54) |
В этом случае грузы смещаются из положения равновесия в одну сторону на одинаковые расстояния. Скорости их также одинаковы по величине и направлению. Соединительная пружина колеблется вместе с грузами, но остается не растянутой и потому не оказывает влияния, так что частота колебаний совпадает с частотой колебаний несвязанных маятников.
В разобранном случае мы познакомились с нормальными модами и выяснили, что их частоты сдвигаются по сравнению с частотами колебаний несвязанных маятников. Любое другое колебательное движение системы можно представить как суперпозицию нормальных мод. Аналогичным образом можно рассмотреть цепочку из множества связанных друг с другом осцилляторов и изучить их нормальные колебания. Такая система представляет собой модель кристаллической решетки.
Поиск по сайту: