 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пружинный маятник
Колебательное движение
Уравнение гармонических колебаний
В этом разделе мы покажем, что уравнения колебательного движения многих систем, в сущности, одинаковы, так что различные физические процессы могут быть описаны одними и теми же математическими формулами.
Пружинный маятник
| Пружинный маятник - это система, состоящая из шарика массой m, подвешенного на пружине. |
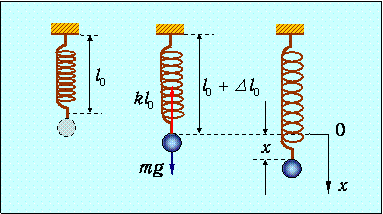
Рис. 1.2. К выводу уравнения движения для пружинного маятника
В положении равновесия (рис. 1.2) сила тяжести mg уравновешивается упругой силой kDl0:

откуда
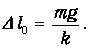
| (1.1) |
где Dl0 – статическое удлинение пружины. Направим ось x вниз и выберем начало отсчета так, что координата x=0 соответствует положению неподвижного шарика в положении равновесия.
Если теперь оттянуть шарик от положения равновесия на расстояние x, то полное удлинение пружины станет равным Dl0+x. По закону Гука результирующая сила будет тогда равна

| (1.2) | |
Учитывая, что  получим получим
| 
| (1.3) |
Знак минус означает, что сила стремится уменьшить отклонение от положения равновесия. Полученное выражение соответствует упругой силе слабо деформированной пружины.
Запишем теперь уравнение второго закона Ньютона:
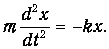
Его можно также представить в виде:
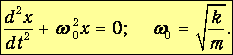
| (1.4) |
Поиск по сайту: