Колебания струны

Рассмотрим малые колебания струны, натянутой силой Т вдоль оси х. Произвольная точка струны с координатой х в момент времени t смещается на вектор u(x, t). Ограничимся простейшим колебательным процессом, когда все векторы смещения u(x, t) в любой момент времени перпендикулярны оси х и лежат в одной плоскости. Тогда смещения точек струны можно описать одной функцией u(x, t), характеризующей вертикальное перемещение струны (рис. 3.1).

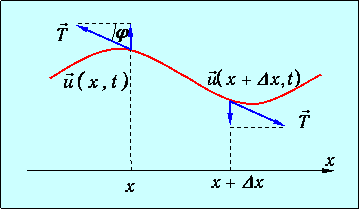
Рис. 3.1. Колебания струны

Напряжения, возникающие в струне, направлены по касательным к ее мгновенному профилю. Мы будем рассматривать малые колебания, когда можно пренебречь удлинением струны и возникающими при этом дополнительными силами упругости. Тогда натяжение струны можно считать постоянным для всех времен t и точек х. Выделим элемент струны, лежащий между координатами х и х+Dх. Рассмотрим точку х. Тангенс наклона силы T, действующей на этот край элемента, равен

Вертикальная компонента силы равна

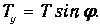
Так как угол j мал, то

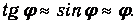
Тогда

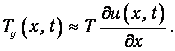
Аналогично, вертикальная компонента силы натяжения струны, действующей на другом конце выделенного элемента, равна

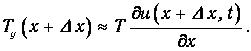
Равнодействующая этих сил равна

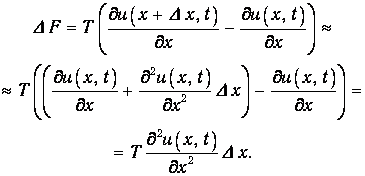
Заметим, что горизонтальные компоненты силы натяжения

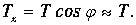
не зависят от положения точки и потому их равнодействующая равна нулю. Это означает, что элементы струны движутся только в вертикальном направлении.

Если линейная плотность (масса единицы длины) струны равна r, то масса элемента равна

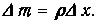
Записываем уравнение второго закона Ньютона для вертикального смещения элемента струны:

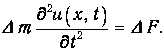
Подставляя сюда выражение для силы DF, получаем уравнение движения струны:

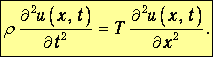
(3.1)

Это уравнение можно переписать в виде:

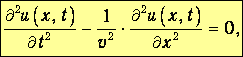
(3.2)

где

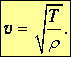
(3.3)

Определим размерность величины v. Размерность силы

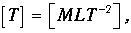
размерность линейной плотности материала струны

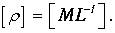
Отсюда размерность величина v будет

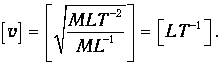
то есть величина v имеет размерность скорости.

Поиск по сайту: