 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Трехмерное волновое уравнение
Пусть мы по-прежнему имеем дело с плоской волной. Повернем координатные оси так, чтобы направление распространения волны задавалось каким-то единичным вектором n. Решение, очевидно, имеет вид:
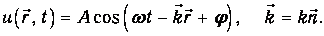
| (3.65) |
Соотношения между w, kи v остаются прежними.
Волновой вектор - это вектор, модуль которого равен волновому числу, а направление совпадает с направлением распространения волны:

|
Фронт волны – плоскость, ортогональная волновому вектору k, – движется со скоростью v, оставаясь параллельным самому себе.
Найдем уравнение, которому удовлетворяет решение (3.65). Дважды дифференцируем выражение (3.65)по координатам х, у, z:

| (3.66) |
Складывая эти три уравнения, находим:

| (3.67) |
Вторая производная решения по времени дает уравнение:

| (3.68) |
Учитывая соотношение

получаем из (3.67), (3.68):
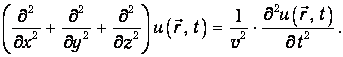
| (3.69) |
Выражение в скобках в левой части уравнения является дифференциальным оператором, который называется лапласианом и имеет специальное обозначение D
Записываем волновое уравнение для волн в трехмерном пространстве в окончательной форме:

| (3.70) |
Если волновая функция и зависит только от одной координаты (скажем, х), то лапласиан превращается во вторую производную по x и мы возвращаемся к прежней форме волнового уравнения.
Подчеркнем, что D не есть греческая буква D («дельта»), а Du не есть приращение величины u, но сумма вторых ее производных по координатам.
Но волновое уравнение (3.70) имеет и другие решения, нежели плоские волны. Простым дифференцированием можно убедиться, что сферическая волна

| (3.71) |
удовлетворяет волновому уравнению. Фронт волны является сферой с центром в месте расположения источника колебаний (r=0), причем радиус сферы увеличивается со скоростью v.
Действительно, поверхность постоянной фазы дается уравнением

дифференцируя которое, находим

Амплитуда сферической волны

убывает с увеличением расстояния до точки наблюдения. Интенсивность волны 
убывает по закону обратных квадратов. Это, как и закон Кулона, также связано с трехмерностью нашего пространства. Если среда не поглощает излучение, то поток энергии через поверхность сферы одинаков для сфер любых радиусов, окружающих источник излучения. Поскольку площадь сферы равна 4pr2, то энергия, проходящая через единицу площади, обратно пропорциональна r2.
Поиск по сайту: