Эффект Доплера для звука

Стоя у полотна железной дороги, можно наблюдать следующее явление: сигнал приближающегося поезда резко меняет свой тон (частоту) в момент прохождения электрички мимо наблюдателя. Это же явление может заметить наблюдатель, сидящий в поезде и проезжающий мимо сигналящего автомобиля, стоящего на переезде.
На рис. 3.18 демонстрируется аналогичное явление при движении вертолета мимо наблюдателя.

Рис. 3.18. Изменение тона звука при движении вертолета мимо наблюдателя

Эффект назван по имени австрийского физика X. Доплера, предсказавшего его теоретически в 1842 г.

Движущийся наблюдатель, покоящийся источник звука. Пусть имеется источник звука, испускающий сферические звуковые волны. На рис. 3.19 показано расположение в пространстве четырех последовательных гребней (максимумов) звуковых волн. Пусть волна имеет частоту n₀, тогда расстояние между гребнями равно длине волны

Рис. 3.19. Эффект Доплера при движении наблюдателя

Наблюдатель А движется прямо на источник звука со скоростью v_H. Поэтому гребни волн приближаются к нему с увеличенной скоростью V=v+v_H. С каждым последовательным гребнем волны наблюдатель встретится через время

после предыдущего. Следовательно, для него изменяется период колебаний. Наблюдаемая частота волны равна

откуда находим:

(3.72)

Наблюдатель В удаляется по прямой линии от источника с той же скоростью v_H (предполагаем, что v_H<v. наблюдатель, удаляющийся от источника со сверхзвуковой скоростью, вообще не услышит звука). Значит, гребни волн приближаются к нему со скоростью V=v-v_H, и период колебаний равен

Отсюда получаем для наблюдаемой частоты:

(3.73)

Наконец, пусть наблюдатель Р движется со скоростью v_H, составляющей угол q с направлением на источник. На сдвиг частоты влияет только компонента скорости вдоль линии, соединяющей наблюдателя и источник:

(3.74)

Предыдущие формулы (3.72) и (3.73) для частных случаев получаются отсюда при q=0 и q=p, соответственно.

На рис. 3.20 с помощью модели демонстрируется эффект Доплера для случая покоящегося источника звука и движущегося наблюдателя.

Рис. 3.20. Моделирование эффекта Доплера при движении наблюдателя

Движущийся источник звука, покоящийся наблюдатель. Пусть теперь наблюдатель неподвижен, а звуковые волны испускаются источником, движущимся со скоростью v_И. На рис. 3.21 показано расположение в пространстве четырех последовательных гребней звуковой волны, отмеченных цифрами черного цвета 1, 2, 3, 4.

Рис. 3.21. Эффект Доплера при движении источника

Эти гребни были испущены, когда источник звука находился в точках, отмеченных цифрами красного цвета 1, 2, 3, 4, соответственно. Иначе, точка 1 является центром сферы 1, точка 2 – центром сферы 2 и т.д. Видно, что центры соседних сфер смещаются на расстояние, проходимое источником за период колебаний

Это приводит к изменению расстояния между гребнями волн, приходящих к наблюдателю. Следовательно, наблюдатель регистрирует иную длину волны.

Наблюдатель А расположен так, что источник движется прямо на него. Для этого наблюдателя расстояние между гребнями волн уменьшается и равно

(3.75)

Скорость волны не зависит от движения источника, поскольку определяется свойствами среды. Следовательно, имеем обычную связь между длиной волны и ее фазовой скоростью:

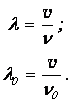
Подставляя эти соотношения в (3.75), получаем

откуда находим частоту nзвука, воспринимаемого наблюдателем А:

(3.76)

Для наблюдателя В расстояние между гребнями волн увеличивается и равно

Аналогичные рассуждения приводят к следующему выражению для частоты звуковой волны:

(3.77)

Наконец, для наблюдателя Р, направление на которого составляет угол j?со скоростью источника, выражение для частоты имеет вид:

(3.78)

Предыдущие выражения получаются отсюда при j=0 и j=p, соответственно.

Пример 1. Наблюдатель, стоящий на платформе железной дороги, слышит гудок проходящего мимо поезда. Когда поезд приближается, частота звуковых колебаний гудка равна n₁, а когда поезд удаляется – n₂. Определим скорость поезда V и собственную частоту гудка n₀. Скорость звука v предполагается известной.

При скорости поезда V, скорости звука v и собственной частоте колебаний n₀ частота n₁, воспринимаемая при приближении поезда, равна

(3.79)

При удалении поезда воспринимаемая частота звука равна

(3.80)

Разделив первое соотношение на второе, получаем:

(3.81)

Отсюда находим скорость поезда:

(3.82)

Подставляя скорость поезда в выражение (3.79), получаем оттуда:

(3.83)

На рис. 3.22 с помощью модели демонстрируется эффект Доплера в случае движущегося источника звука и покоящегося наблюдателя.

Рис. 3.22. Моделирование эффекта Доплера при движении источника

Движущийся источник звука, движущийся наблюдатель. Из полученных формул можно сделать общие выводы:

· для изменения частоты воспринимаемого звука при движении источника или наблюдателя важны не абсолютные значения скоростей, а скорости сближения (удаления), то есть проекции скоростей на линию, соединяющую источник и наблюдателя;

· при сближении источника с наблюдателем частота звука увеличивается, при удалении – уменьшается;

· сли движутся и источник, и наблюдатель, то следует объединить формулы (3.74) и (3.78), а также (3.72) и (3.76):

(3.84)

· в формуле (3.84), в соответствии со сказанным, под скоростями v_H и v_И надо понимать теперь не абсолютные скорости наблюдателя и источника, а их проекции на линию, соединяющую источник и наблюдателя: положительные знаки скоростей соответствуют сближению, отрицательные – удалению источника и наблюдателя.

Выражение (3.84) явным образом нарушает принцип относительности Галилея. В самом деле, скорость v_OTH сближения источника и наблюдателя есть сумма соответствующих проекций скоростей:

Согласно принципу относительности, все наблюдаемые эффекты должны зависеть только от v_OTH. Формула же (3.84) позволяет отделить движение наблюдателя от движения источника. Для иллюстрации рассмотрим три примера.

Пример 2. Сирена полицейской машины, стоящей на обочине дороги, издает сигнал на частоте 1 000 Гц. Определим, звук какой частоты услышит водитель, проезжающий мимо со скоростью 80 км/час.

В данном случае скорость автомобиля V=80 км/час=22.2 м/с – это скорость наблюдателя. Скорость звука 343 м/с. При сближении с полицейской машиной водитель воспринимает звук частотой

После того как водитель миновал полицейскую машину, воспринимаемая частота становится равной

Пример 3. Водитель стоящей на обочине дороги машины замечает проезжающий мимо полицейский автомобиль с включенной сиреной. Найдем частоту звука, который слышит водитель, если скорость полицейского автомобиля равна 80 км/час. Полицейская сирена – та же самая, что и в предыдущем примере.
Здесь скорость V=22.2 м/с – это скорость движения источника. При приближении полиции водитель слышит сигнал частотой

При удалении частота воспринимаемого сигнала равна

Пример 4. Те же машины едут навстречу друг другу с равными скоростями 40 км/час=11.1 м/с. Найдем частоты звукового сигнала при сближении и при удалении машин.

Применяем формулу (3.84). При сближении воспринимается звук частотой

При удалении машин сирена для водителя звучит на частоте

Во всех трех случаях получились разные результаты, хотя каждый раз скорости сближения (удаления) наблюдателя и источника были теми же самыми. В то же время численные результаты близки друг к другу. Это объясняется тем, что скорости автомобилей в задаче малы по сравнению со скоростью звука. В этом случае в формуле (3.84) можно пренебречь членами

и более высоких степеней. Преобразуем (3.84):

Пренебрегая теперь слагаемыми, содержащими отношения квадратов скоростей, находим приближенное выражение:

(3.84)

В (3.85) частота зависит только от относительной скорости источника и наблюдателя. Если бы формула была точна, во всех трех задачах мы получили бы один и тот же ответ:

Формула (3.85) удовлетворяет принципу относительности Галилея, но она верна, строго говоря, только при бесконечно большой скорости сигнала. Нарушение принципа относительности Галилея связано с наличием среды. Действительно, при движении тел в среде можно отличить состояние покоя от прямолинейного равномерного движения хотя бы по возникающему при движении ветру. Поэтому системы отсчета при наличии среды не равноправны: из них выделена та, в которой среда как целое покоится.

Поиск по сайту: