 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Гармонические колебания. Мы рассмотрели несколько совершенно различных систем, и убедились, что уравнения движения приводятся к одной и той же форме (1.18)
Мы рассмотрели несколько совершенно различных систем, и убедились, что уравнения движения приводятся к одной и той же форме

| (1.18) |
Разница между физическими системами заключена в определении величины w0 и в физическом смысле переменной x: это может быть координата, угол, заряд, ток и т.д. Уравнение (1.18) описывает так называемые гармонические колебания.
| Гармонические колебания -это такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону синуса или косинуса. |
Уравнение гармонических колебаний (1.18) является линейным дифференциальным уравнением второго порядка (так как оно содержит вторую производную от переменной x). Линейность уравнения означает, что
· если какая-то функция x(t) является решением этого уравнения, то функция Cx(t) также будет его решением (C – произвольная постоянная);
· если функции x1(t) и x2(t) являются решениями этого уравнения, то их сумма x1(t) + x2(t) также будет решением того же уравнения.
Доказана также математическая теорема, что уравнение второго порядка имеет два независимых решения. Все остальные решения, согласно свойствам линейности, могут быть получены как их линейные комбинации. Непосредственным дифференцированием легко проверить, что независимые функции sinw0t и cosw0t удовлетворяют уравнению (1.18). Значит, общее решение этого уравнения имеет вид:
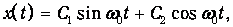
| (1.19) |
где C1, C2 – произвольные постоянные. Это решение может быть представлено и в другом виде. Введем величину

| (1.20) |
и определим угол a соотношениями:

| (1.21) |
Тогда общее решение (1.19) записывается как

| (1.22) |
Согласно формулам тригонометрии, выражение в скобках равно

Окончательно приходим к общему решению уравнения гармонических колебаний в виде:

| (1.23) |
Величина A называется амплитудой колебания, а a – начальной фазой. Вся комбинация w0t+a называется фазой колебания.
На рис. 1.7 демонстрируется временн а я развертка гармонических колебаний математического маятника.

Рис. 1.7. Временная развертка гармонических колебаний математического маятника
Выражения (1.19) и (1.23) совершенно эквивалентны, так что мы можем пользоваться любым их них, исходя из соображений простоты. Оба решения являются периодическими функциями времени. Действительно, синус и косинус периодичны с периодом 2p. Поэтому различные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени t*, за который фаза колебания получает приращение, кратное 2p:

| (1.24) |
Отсюда следует, что

Наименьшее из этих времен
 (1.25)
(1.25)
называется периодом колебаний (рис. 1.8), а w 0 – его круговой (циклической) частотой.
Равномерное движение по окружности также можно рассматривать как колебательный повторяющийся процесс (рис. 1.8). В этом случае w0 совпадает с угловой скоростью вращения.
Используют также и частоту колебаний

| (1.26) |
| Частота колебаний n0 – это число колебаний, которое совершает система в единицу времени (в частности, в системе СИ – за секунду). |
Соответственно, круговая частота равна числу колебаний за 2p секунд.
| В системе СИ единицей измерения частоты (круговой частоты) являются обратные секунды, для которых введено специальное название – герц (1 Гц=1/c). |
Итак, если система в момент времени t характеризуется значением переменной x(t), то то же самое значение переменная будет иметь через промежуток времени T=2p/w0 (рис.1.9), то есть 
Это же значение, естественно, повторится через время 2T, ЗT и т.д.

Рис. 1.9. Период колебаний
В общее решение входят две произвольные постоянные (C1, C2 или A, a), значения которых должны определяться двумя начальными условиями. Обычно (хотя и не обязательно) их роль играют начальные значения переменной x(0) и ее производной dx/dt.
Приведем пример. Пусть решение (1.19) уравнения гармонических колебаний описывает движение пружинного маятника. Значения произвольных постоянных зависят от способа, каким мы вывели маятник из состояния равновесия. Например, мы оттянули пружину на расстояние x0 и отпустили шарик без начальной скорости. В этом случае

Подставляя t=0 в (1.19), находим значение постоянной С2

Решение, таким образом, имеет вид:

Скорость груза находим дифференцированием

Подставляя сюда t = 0, находим постоянную С1:

откуда

Окончательно

Сравнивая с (1.23), находим, что x0 – это амплитуда колебаний, а его начальная фаза равна нулю: a = 0.
Выведем теперь маятник из равновесия другим способом. Ударим по грузу, так что он приобретет начальную скорость v0. Имеем тогда другие начальные условия:
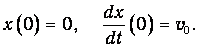
Так как

наше решение имеет вид

Скорость груза будет изменяться по закону:

Подставим сюда t=0:

откуда

Окончательно получаем:
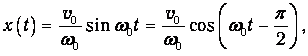
так что амплитуда колебаний равна

а начальная фаза

В общем случае, когда маятник оттягивается на расстояние x0 и отпускается с начальной скоростью v0, связь начальных условий с амплитудой колебаний и начальной фазой имеет вид:

| (1.27) |
Дифференцируя решение (1.22) по времени, найдем зависимость от времени скорости и ускорения маятника:
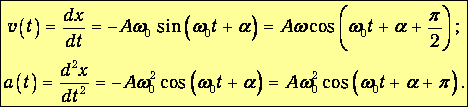
Соответствующие графики представлены на рис. 1.10 (для простоты мы положили начальную фазу a=0). Видно, что скорость и ускорение также изменяются по гармоническому закону, причем амплитуда скорости равна Aw0, а амплитуда ускорения -Аw02. Скорость опережает смещение по фазе на p/2, ускорение находится в противофазе по отношению к смещению. Это означает, что в тот момент, когда смещение достигает наибольшего значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот.

Рис. 1.10. Зависимость от времени положения, скорости и ускорения колеблющейся материальной точки
Поиск по сайту: