Сверхзвуковые скорости

Рассмотрим теперь случай, когда источник звуковых волн движется со скоростью, превышающей скорость звука: v_И>v. Пусть в момент времени t=0 источник был в точке S₀, а в момент t он находится в точке S_t (рис. 3.23). Расстояние между этими точками равно v_Иt.

Рис. 3.23. Образование конуса Маха при сверхзвуковом движении источника

В каждой точке своей траектории (для простоты мы рассматриваем прямолинейное равномерное движение) источник испускал сферические звуковые волны. Волна, испущенная в момент t = 0, к текущему моменту времени t достигла точки А. Волны, испущенные на пути от S₀ до S_t,успели пройти меньшее расстояние. Как видно из рис. 22.14, в данный момент времени имеется коническая поверхность (ее называют конусом Маха ), касательная к фронтам всех испущенных сферических волн. Эта коническая поверхность начинается от источника звука, а ее ось совпадает с направлением движения источника. Конус Маха отделяет области пространства, куда дошел звук от источника, от тех областей, куда звук не успел еще дойти. В следующий момент времени t+Dt источник переместится в точку S_t+Dt. Соответственно переместится и конус Маха, захватив новые области пространства (показано пунктирной линией).

Синус угла раствора конуса определяется как отношение расстояния vt, пройденного звуковой волной за время t, к расстоянию v_Иt, пройденного источником за то же время:

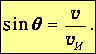
(3.86)

Коническую поверхность можно воспринимать как фронт волны (ее называют ударной). Направление распространения волны – это нормаль к фронту. Следовательно, ударная волна распространяется под углом

к направлению движения источника. Соответственно, (3.86) можно записать в виде:

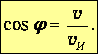
(3.87)

Пример 5. Самолет летит горизонтально на высоте 5 000 м с постоянной скоростью. Наблюдатель заметил его у себя над головой, и засек время. Звук от самолета появился через 11 с после этого. Найдем скорость самолета и определим, на каком расстоянии по горизонтали находится самолет от наблюдателя в момент, когда последний зарегистрировал приход звука от него?

За время t самолет удалился от наблюдателя на расстояние s=Vt. Так как в этот момент звук достиг наблюдателя, то точка наблюдения оказалась на конусе Маха (рис. 3.24).

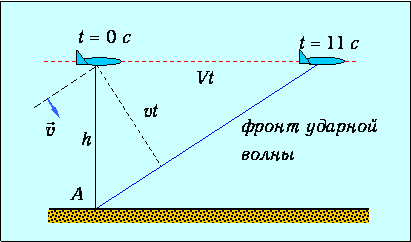
Рис. 3.24. К примеру 5. О пролете сверхзвукового самолета. Пунктирная линия – положение конуса Маха в момент пролета самолета над головой, сплошная – конус Маха в момент, когда звук дошел до наблюдателя

Имеем соотношения:

(3.88)

Отсюда:

(3.89)

Используя соотношение

получаем связь скорости самолета с высотой полета и временем t:

откуда:

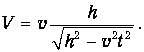
(3.90)

Подставляем числовые данные:

(3.91)

Число Маха (здесь v_И=V) равно

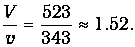
При такой скорости движения самолет удалился по горизонтали на расстояние

Заметим, кстати, что момент прихода к наблюдателю фронта ударной волны воспринимается как резкий хлопок (подобный грому). Бытующее выражение «самолет преодолел звуковой барьер» неверно отражает физический процесс: хлопок, как мы видели, не связан с моментом, когда самолет приобрел сверхзвуковую скорость.
На рис. 3.25 демонстрируется прохождение ударной волны при движении сверхзвукового самолета.

Рис. 3.25. Прохождение ударной волны при движении сверхзвукового самолета

Проанализируем формулу (3.90). Видно, что время задержки t не может быть больше, чем

Такая задержка могла бы быть при очень большой скорости самолета (V>>v), когда конус Маха становится крайне узким, почти параллельным направлению движения. Фронту ударной волны, распространяющемуся вертикально вниз, надо при этом пройти расстояние h, что он и осуществляет за время t_MAX.
Время задержки t =0 соответствует случаю, когда скорость самолета равна скорости звука: V=v. При этом угол раствора конуса Маха становится равным p/2 (рис. 3.26), так что ударная волна доходит до наблюдателя в тот самый момент, когда самолет оказывается у него над головой.

Рис. 3.26. Фронт ударной волны в случае движения источника со скоростью звука. В каждый момент времени t источник находится на поверхности всех сферических волн, испущенных ранее. Огибающая этих сферических волн – фронт ударной волны – представляет собой плоскость, ортогональную направлению движения источника

При дозвуковых скоростях звук опережает летательный аппарат и приходит к наблюдателю раньше самолета.

Поиск по сайту: