АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Математический маятник

Читайте также:
  1. Африканский континент: «закон маятника»
  2. Б) Математический утренник.
  3. Введение в математический анализ.
  4. Вопрос 26 : Свободные гармонические механические колебания и их характеристики. Математический и физический маятники.
  5. Вывод: чем больше автомобилей в обществе, тем больше времени – начиная с определенного рубежа — люди будут тратить и терять на поездки. Это математический факт.
  6. Гайка крепления оси маятниковой вилки
  7. Доказать возможность гармонических колебаний для пружинного маятника и определить все их характеристики и необходимые условия.
  8. МАТЕМАТИЧЕСКИЙ АНАЛИЗ.
  9. МАТЕМАТИЧЕСКИЙ ИДЕАЛ
  10. Математический инструментарий принятия решения
  11. Математический инструментарий прогнозирования
Математический маятник - это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.  

Будем характеризовать отклонение маятника от положения равновесия углом j, который образует нить с вертикалью (рис. 1.3).

Рис. 1.3. К выводу уравнения движения математического маятника

При отклонении маятника от положения равновесия на материальную точку массой m действуют сила тяжести m g и сила натяжения нити T. Их равнодействующая F направлена по касательной к окружности радиусом l и равна

Скорость материальной точки тоже направлена по касательной и равна

так что тангенциальное ускорение будет

Записываем теперь уравнение движения

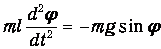
  (1.5)

(знак минус соответствует тому, что сила F стремится уменьшить угол j). При небольших отклонениях маятника

Получаем тогда:

  (1.6)

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)