Колебания в твердых телах

Колебательные процессы в твердых телах похожи на колебания в газах. На рис. 3.3 представлена продольная деформация твердого тела в направлении оси х.

Рис. 3.3. Продольные колебания в твердом теле

Относительная деформация элементарного объема при смещении u равна

Согласно закону Гука, это приводит к появлению упругой силы

(3.10)

где Е – коэффициент (модуль Юнга), характеризующий жесткость среды. Равнодействующая сил упругости, действующих в сечениях 1' и 2' равна:

(3.11)

Записывая второй закон Ньютона в виде:

(3.12)

находим уравнение колебаний в твердом теле:

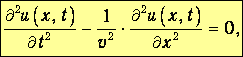
(3.13)

где

(3.14)

Размерность модуля Юнга совпадает с размерностью давления, так что v и здесь имеет размерность скорости.

Выше мы рассматривали продольные смещения в твердом теле. В отличие от газов, упругие силы возникают в твердых телах и при деформации сдвига. Уравнение для таких поперечных колебаний имеет тот же вид (3.13), но вместо модуля Юнга в выражении для v будет стоять так называемый модуль сдвига G:

(3.15)

Механизм распространения продольных и поперечных колебаний показан на рис. 3.4 и 3.5.

Рис. 3.4. Продольные волны в твердом теле

Рис. 3.5. Поперечные волны в твердом теле

Поиск по сайту: