Колебания поршня в сосуде с идеальным газом

Рассмотрим поршень массой m и площадью поверхности S, прикрывающий сосуд объемом V₀ с идеальным газом, изолированным от окружающей среды (рис. 1.5).

Рис. 1.5. Колебания поршня, закрывающего сосуд с идеальным газом

Пусть в состоянии равновесия давление в сосуде равно p₀. Это давление складывается из атмосферного давления p _А и давления mg/S, оказываемого поршнем:

(1.10)

Переместим поршень на расстояние x. Объем сосуда увеличится и станет равным

Соответственно уменьшится давление. Новое давление можно найти из уравнения адиабаты Пуассона

откуда

(1.11)

Здесь g – показатель адиабаты, зависящий от числа степеней свободы молекул газа.

При малых колебаниях, когда смещения поршня много меньше высоты сосуда

можно разложить р в ряд Тейлора:

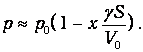
(1.12)

На поршень действуют три силы: сила атмосферного давления p_АS, сила давления газа в сосуде pS и сила тяжести mg. Знаки сил соответствуют выбору положительного направления оси x вверх. Используя (1.10) и (1.12), находим для равнодействующей Fэтих сил:

(1.13)

Записываем теперь уравнение движения поршня

в виде

(1.14)

Поиск по сайту: