Молекулярные спектры

По сравнению с линейчатыми атомными спектрами молекулярные имеют более сложную структуру. Они состоят из совокупности полос, которые, в свою очередь, распадаются на ряд тесно расположенных линий. Причина такого усложнения спектров заключается в том, что наряду с движением электронов вокруг ядер в молекуле происходит колебание самих ядер относительно положения равновесия и вращение молекул как целого. Этим трем видам движений соответствуют три типа квантовых уровней энергии: электронные, колебательные и вращательные. В первом приближении движения можно считать независимыми. При изучении молекулярных спектров чрезвычайно важно то обстоятельство, что масса ядра более чем на три порядка превосходит электронную:

Поэтому скорости движения ядер в молекуле малы по сравнению со скоростями электронов. Движение электронов мгновенно приспосабливается к изменению расположения ядер. Таким образом, конфигурацию ядер можно рассматривать как параметр при определении уровней энергии Е_эл. Полная энергия молекулы Е складывается, соответственно, из трех квантованных значений энергий

(6.15)

Электронные уровни энергии. Молекула, подобно атому, обладает рядом возбужденных состояний, различающихся строением электронной оболочки. Переходы электрона из одного состояния в другое связаны с поглощением или испусканием квантов света. Порядок энергии электронных уровней молекулы можно оценить из соотношения неопределенностей Гейзенберга, аналогично тому, как была получена энергия основного состояния атома водорода. Если линейные размеры молекулы водорода R₀, то энергия уровня

(6.16)

что при типичных значениях

составляет несколько электрон-вольт и соответствует переходам с испусканием квантов в видимой и ультрафиолетовой областях спектра.

Энергия колебательного движения ядер. Движение ядер в молекуле можно рассматривать при заданном электронном состоянии. Изучение относительного движения ядер с массами М₁ и М₂ в молекуле сводится к решению задачи о поведении частицы с приведенной массой

в потенциальном поле. Для заданного связанного электронного состояния молекулы энергия E(R) имеет минимум, когда ядра расположены на расстоянии R₀. Разложим E(R) в ряд Тейлора вблизи точки минимума по степеням (R-R₀):

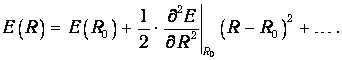
(6.17)

С точностью до постоянной E(R₀) энергия движения ядер пропорциональна квадрату расстояния от положения равновесия. Следовательно, эти атомы колеблются под действием квазиупругой силы

(6.18)

Квантовая механика (см. разд. 3.3) позволяет определить энергетические состояния такой колебательной системы (гармонического осциллятора), которые образуют совокупность эквидистантных (равноотстоящих) уровней:

(6.19)

где u - колебательное (вибрационное) квантовое число, а частота

совпадает с частотой классического осциллятора. Переходы между колебательными уровнями подчиняются правилу отбора

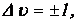
то есть вибрационное число при переходе может измениться лишь на единицу.

Для оценки порядка величины энергии колебательного движения заметим, что при амплитуде колебаний порядка расстояния R₀ между ядрами молекула диссоциирует (разваливается). Энергия таких колебаний составляет величину порядка

С другой стороны, изменение энергии при амплитуде колебаний R₀ близко к величине электронной энергии Е_эл Действительно, изменение межъядерного расстояния на величину R₀ должно вызывать существенные искажения электронной волновой функции y₊, то есть возбуждение электронов с изменением их энергии на величину порядка Е_эл. Таким образом, получаем оценку «коэффициента жесткости» молекулярного осциллятора:

(см. соотношение (6.11)), а также энергии колебательного движения

(6.20)

Это величина порядка десятых или сотых долей электрон-вольта и соответствует излучению в инфракрасной области спектра. Таким образом, колебательная энергия много меньше энергии электронного уровня.

Энергия вращательного движения молекул. Вращение молекул рассмотрим в предположении жесткой связи между ядрами, то есть пренебрегая колебаниями. Для двухатомной молекулы момент инерции относительно оси, перпендикулярной оси молекулы и проходящий через центр инерции, равен

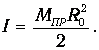
Согласно законам механики, энергия вращательного движения связана с вращательным моментом импульса L молекулы выражением

Вращательный момент квантуется:

где J=0, 1, 2,... - ротационное квантовое число. Это позволяет определить вращательные уровни энергии:

(6.21)

Отсюда следует оценка величины вращательной энергии:

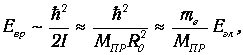
(6.22)

то есть величину порядка

соответствующую излучению в далекой инфракрасной и микроволновой (СВЧ) областях спектра. Для вращательного спектра разрешены переходы с

Молекулярные спектры. Проведенные оценки величины трех типов уровней в молекуле показывают, что

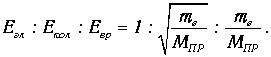
(6.23)

В соответствии с этими отношениями система уровней молекулы складывается из сравнительно далеко отстоящих электронных уровней, испытывающих расщепление под влиянием колебаний ядер. Эти расщепленные уровни, в свою очередь, испытывают еще более тонкое расщепление в связи с вращением молекул (рис. 6.8).

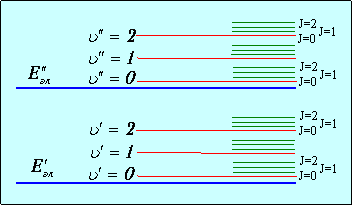
Рис. 6.8.Схема расположения электронных, вращательных и колебательных уровней энергии молекулы

Изменение электронного состояния молекулы связано обычно с целой серией изменений: колебательное движение претерпевает изменения, так как новому состоянию соответствует измененное равновесное расстояние между ядрами; при этом также изменяется и момент инерции молекулы и, следовательно, положение вращательных уровней. Эти изменения вызывают целую серию поглощаемых или испускаемых квантов, энергии которых соответствуют разнице энергий каких-либо уровней, между которыми происходит переход.

Если атомные спектры состоят из отдельных линий, то при наблюдении с низким разрешением молекулярные спектры представляются состоящими из полос. При применении приборов с высокой разрешающей способностью обнаруживается, что полосы состоят из большого числа тесно расположенных линий. В соответствии с их характером спектры молекул носят название полосатых спектров. В зависимости от того, изменение каких видов энергии (электронной, колебательной или вращательной) вызывает испускание молекулой фотона, различают следующие типы полос: 1) вращательные; 2) колебательно-вращательные; 3) электронно-колебательные.

В основном состоянии молекулы все три вида энергии имеют минимальное значение. При сообщении молекуле достаточного количества энергии она переходит в возбужденное состояние и затем, совершая разрешенный правилами отбора переход в одно из более низких энергетических состояний, излучает фотон с энергией

(6.24)

Следует отметить, что значения частоты w_кол и момента инерции I зависят от электронных конфигураций молекулы и поэтому обозначены одним и двумя штрихами.

Учитывая соотношения между энергиями

приходим к выводу, что при слабых возбуждениях изменяется только Е_вр при более сильных - Е_кол, и лишь при еще более сильных возбуждениях изменяется электронная конфигурация молекулы, то есть Е_эл. Соответственно, наименьшей энергией обладают фотоны, связанные с вращательными переходами (электронная конфигурация и энергия колебательного движения не изменяются). Учитывая, что DJ= + 1, находим

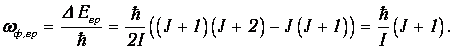
(6.25)

Измерение энергии таких фотонов позволяет определить момент инерции молекулы и, следовательно, ее размер R₀. Например, для НCl найдено I=2.71 · 10^-47 кг · м², что соответствует R₀=1.29 · 10^-10 м.

При переходах, сопровождающихся изменениями и колебательного, и вращательного состояний молекулы, частота излучаемого фотона может быть записана в виде

(6.26)

где было учтено, что Du= + 1.

Поиск по сайту: