Уравнение Шредингера для простейших систем

Свободная частица, движущаяся вдоль оси х

Потенциальная энергия равна нулю: U(x)=0, и производные по у и z в операторе Лапласа исчезают. Уравнение (4.19) принимает вид

Введем волновой вектор k, обозначив

и перепишем уравнение в виде

(4.22)

Существуют, как известно, два линейно независимых решения уравнения (4.22), так что общее решение есть суперпозиция двух волн - или стоячих:

или бегущих:

(первый член - волна бежит направо, второй - налево; постоянные А и В произвольны). Аналогия: такие же решения описывают колебания свободной струны. Поскольку возможны волны с произвольной частотой, струна не звучит (то есть энергия частицы принимает любые значения - не квантуется). Для частицы, движущейся в произвольном направлении вдоль волнового вектора k, справедливы те же решения при замене

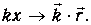
При решении большинства задач квантовой механики следует обратить внимание на то, что волновая функция должна быть непрерывной - вероятность пребывания частицы не может меняться скачком от точки к точке. Если потенциальная энергия конечна, то из уравнения Шредингера следует, что первая производная волновой функции также непрерывна.

Поиск по сайту: