 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Атом водорода
Стационарное уравнение Шредингера для водородоподобного атома (один электрон около ядра с зарядом Ze) имеет вид

Это уравнение удобно записать в сферических координатах:

| (5.6) |
Разумеется, мы не станем решать это уравнение, но просто внимательно на него посмотрим.
Заметим, что та часть уравнения (5.6), которая зависит от углов, входит только в состав оператора квадрата момента импульса Довольно ясен физический смысл этого члена. Представим себе, что в поле центральных сил по орбите радиусом r движется классическая частица с импульсом р. Ее момент количества движения равен

где р | - проекция импульса на направление, ортогональное радиусу-вектору r. Обозначим

кинетическую энергию «ортогонального» движения. Ее можно выразить через квадрат момента количества движения:

Этот член добавляется к потенциальной энергии кулоновского притяжения к ядру, и его можно интерпретировать как потенциальную энергию в поле центробежных сил. Действительно, если K | - потенциальная энергия, то ее производная по r должна дать соответствующие силы:

В конечном выражении легко узнать известную из классической механики формулу для центробежной силы. Квантовая механика, как это и должно быть, воспроизводит на новом уровне результаты классической: теперь момент импульса стал оператором, но вошел на прежних правах в выражение для оператора полной энергии (гамильтониана).
Любой оператор коммутирует сам с собой, и так как оператор квадрата момента (5.3) вообще не зависит от радиальной переменной r, то

коммутирует с гамильтонианом из уравнения Шредингера (5.6). Кроме того, оператор проекции момента импульса

коммутирует c

и, стало быть, с гамильтонианом из уравнения Шредингера. Следовательно, выполняются классические законы сохранения квадрата и одной проекции момента импульса. Эти законы сохранения справедливы для любого центрально-симметричного поля: специфика кулоновского взаимодействия пока нами не использовалась. Поэтому проекция и квадрат момента могут быть определены одновременно с энергией, и волновая функция стационарного состояния будет зависеть от квантовых чисел l и т. Однако в уравнении Шредингера (5.6) гамильтониан вовсе не зависит от оператора проекции момента импульса. Это значит, что энергия состояния не будет зависеть от магнитного квантового числа т. Иными словами, в любом центрально-симметричном поле имеется вырождение по т, кратность которого равна 21+1. Мы уже знаем, что источником вырождения должна служить та или иная симметрия. В классической физике движение частицы в центрально-симметричном поле всегда происходит по орбите, лежащей в одной плоскости. Но сама эта плоскость может быть произвольной в зависимости от начального положения и скорости частицы. Ясно, что значение полной энергии частицы не зависит при этом от ориентации плоскости орбиты в пространстве. Это и есть искомая симметрия, приводящая к вырождению по магнитному квантовому числу.
В кулоновском поле (равно как и в гравитационном) имеется еще одно специфическое вырождение, приводящее к тому, что энергия системы не зависит и от квантового числа l.
Вспомним опять классическую физику. В кулоновском поле финитное движение частицы совершается только по эллипсу. Возьмем в качестве аналогии искусственный спутник. Поместим его на каком-то расстоянии от Земли (то есть зададим потенциальную энергию) и придадим ему какую-то скорость (зададим кинетическую энергию). Таким образом, мы задали полную энергию спутника. Но определена ли его орбита? Разумеется, нет! При той же полной энергии направление скорости влияет на форму орбиты - от прямой линии (вертикальное падение) при нулевом моменте импульса до максимально возможного при данной полной энергии. Нулевой момент соответствует чисто радиальным колебаниям сквозь центр притяжения, когда вовсе нет кругового движения, и эллипс вырождается в прямую линию (для спутника такое колебание невозможно, но микрочастицы - иное дело). Максимально возможный момент импульса достигается в обратном случае чисто круговой орбиты, когда совсем нет радиального движения. Важно, что его величина зависит от полной энергии спутника.
Итак, классическая физика подсказывает нам следующие свойства решений уравнения Шредингера:
| · энергия электрона не должна зависеть от квантовых чисел l, т; · квантовое число l должно пробегать ряд целых значений от нулевого до максимального; · максимальное значение l должно зависеть от энергии электрона. |
Вооружившись знанием классической механики, мы можем смело приступать к изучению квантовой. Теперь станут понятны свойства решений уравнения Шредингера для атома водорода. Его решениями являются волновые функции, нумеруемые тремя квантовыми числами: п, l, т. Про l и т уже много говорилось, а n - знакомое нам по атому Бора главное квантовое число, принимающее целые положительные значения. Разным наборам чисел п, l, т отвечают разные волновые функции, вид которых нам сейчас не важен.
Пример 1. Волновая функция основного состояния электрона в атоме водорода имеет вид

Найдем вероятности W1 и W2 обнаружить электрон внутри сфер с радиусами аВ и 2аВ.
Вероятность обнаружить электрон в элементе объема dV равна

Так как волновая функция основного состояния не зависит от направления радиуса-вектора r, а лишь от его величины r, то можно написать выражение для вероятности dWr обнаружить электрон в шаровом слое радиусом r и толщиной dr. Объем этого слоя равен dV=4pr2dr (площадь поверхности, умноженная на толщину).Тогда
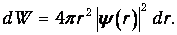
Теперь надо проинтегрировать вероятность dWr no всем значениям r от 0 до R, получив вероятность W(R) найти электрон внутри сферы радиусом R:

Интеграл берется точно, и в результате получаем

| (5.7) |
откуда находим

Здесь е - основание натурального логарифма. Разность W2-W1=0.439 дает вероятность найти электрон между сферами с радиусами аB и 2аB. Видно, что численно эта вероятность имеет тот же порядок величины, что и вероятность W1 Зато вероятность обнаружить электрон за пределами сферы радиусом 2аB заметно меньше: она равна, как нетрудно догадаться,
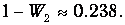
Иными словами, с вероятностью более 76% электрон в основном состоянии пребывает на расстоянии не более двух радиусов Бора.
Пример 2. Найдем электростатический потенциал, создаваемый атомом водорода в основном состоянии.
Возьмем любую точку на расстоянии R от ядра. Электростатический потенциал в ней создается, во-первых, положительным зарядом е ядра и, во-вторых, той частью заряда электрона, которая находится внутри сферы радиусом R. Хорошо известно, что сферически симметричное распределение заряда не создает поля во внутренних областях. Поэтому часть электронного облачка, находящаяся дальше выбранной точки, не внесет вклада в потенциал. Поскольку в уравнении (5.7) вычислена вероятность W(R) нахождения электрона внутри сферы радиусом R, то отрицательный заряд внутри этой сферы равен eW(R). Поэтому потенциал в точке R, создаваемый эффективным зарядом
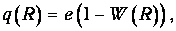
имеет вид
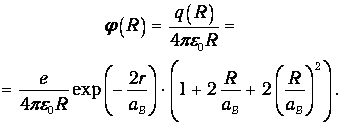
| (5.8) |
На больших расстояниях потенциал (5.8) убывает экспоненциально, то есть гораздо быстрее обычного кулоновского потенциала точечного заряда. Это - так называемый эффект экранировки: отрицательный заряд электрона компенсирует положительный заряд ядра. При

потенциал (5.8) переходит в обычный кулоновский потенциал: мы проникли внутрь электронного облачка, где оно уже не экранирует заряд ядра.
Для энергии из уравнения Шредингера получается в точности такая же формула, что и из теории Бора:

| (5.9) |
Как видно, энергия действительно не зависит от квантовых чисел l, т. При этом, как следует из свойств решений уравнения (5.6), азимутальное квантовое число l принимает целые значения от 0 до п-1. И это свойство, угаданное нами на основе классической физики, воспроизвелось в квантовой механике.
Удивительно, как квантовая механика, низвергнувшая столько классических представлений, дает аналогичные результаты там, где в дело вступают свойства симметрии системы. Отсюда вывод: симметрия играет более важную роль, чем конкретные физические законы. Когда-нибудь будут открыты новые законы, которые обобщат и квантовую механику, и все теории, которые ныне находятся на переднем крае науки. Но свойства симметрии системы так или иначе проявят себя.
Отличие квантовой механики от теории Бора - более богатая структура уровней: состояние определяется тремя квантовыми числами, как и в трехмерном потенциальном ящике. Кстати, это не случайно. Три квантовых числа в потенциальной яме и в атоме водорода - отражение трехмерности нашего пространства. Подсчитаем кратность вырождения, то есть число различных состояний с одной и той же энергией (главным квантовым числом п). При данном значении п число l пробегает все целые числа от 0 до n-1, и каждому из них соответствует 2l+1 значение т. Поэтому кратность вырождения N определяется соотношением

| (5.10) |
При п=1 имеем N=1, то есть основной уровень не вырожден. При п=2 кратность вырождения равна 4: один уровень с l=0 и три уровня с l=1 и различными проекциями момента импульса т=-1, 0, +1. При п=3 кратность вырождения N=9: один уровень с l=0, три уровня с l=1 и пять уровней (по числу проекций) с l=2. Для классификации уровней энергии по значению квантового числа l применяют условные обозначения, позаимствованные из спектроскопии, где они появились еще до создания теории атома:
| l= | 0 | 1 | 2 | 3 | 4 | 5 | … |
| символ | s | p | d | f | g | h | … |
Главное квантовое число ставится впереди символа. Примеры возможных состояний:
1s, 2s, 2p, 3s, Зр, 3d, 4s, 4р, 4d, 4f и т. д.
При переходе электрона с более высокого уровня энергии на более низкий излучается фотон, уносящий собственный угловой момент, равный h (авторы просят принять это на веру). Следовательно, разрешены только переходы с изменением l на единицу: возникает правило отбора
При переходах электрона в атоме с одного энергетического уровня на другой азимутальное квантовое число изменяется на единицу

|
Это значит, что в атоме водорода допустимы переходы
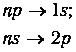
и т. д., приводящие к тем же спектральным сериям, что и теория Бора. Более богатая структура уровней не проявляется пока в большем разнообразии атомных спектров из-за вырождения.
Говоря о вырождении уровней, мы имели в виду водородоподобный атом. В более сложных атомах или в присутствии внешних электромагнитных полей вырождение, как говорят, снимается и появляется зависимость энергии от чисел l, т. Любая не кулоновская центрально-симметричная поправка к потенциальной энергии приведет к зависимости уровней энергии от l (наблюдается в щелочных металлах). В классической физике такая поправка к обычному закону притяжения (например, планеты к Солнцу) превращает эллиптические орбиты в незамкнутые кривые. Обращаясь по таким орбитам, планета как бы движется по обычному эллипсу, который дополнительно вращается как целое, прецессирует в той же плоскости. Подобный эффект - вращение перигелия Меркурия - предсказала общая теория относительности. Новое движение приводит к дополнительной энергии вращения, зависящей от l. В результате энергия уровня 2s перестанет совпадать с энергией уровня 2р и т. д.
Любое не центрально-симметричное поле (например, магнитное) снимет вырождение по т. В классической физике магнитное поле вызывает прецессию плоскости вращения вокруг направления поля и также появление из-за этого вращения дополнительной энергии. Сказанное можно сформулировать в виде общего вывода:
Поиск по сайту: