 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Принцип Паули и валентность элементов
Мы видели, что орбитальный момент импульса характеризуется азимутальным квантовым числом, принимающим целые значения. Собственный спиновый момент электрона характеризуется спиновым квантовым числом s, равным 1/2. Спин - фундаментальное квантовое свойство всех элементарных частиц. В соответствии со значением спинового квантового числа s частицы делятся на два класса: бозоны (целые s) и фермионы (полуцелые s). Другие значения s науке не известны. Примеры фермионов: электрон, мюон, нейтрино, кварки, частицы из трех кварков (протон, нейтрон). Примеры бозонов: фотон, недавно открытые частицы W± и Z, частицы из двух кварков (p -мезоны и др.).
Бозоны и фермионы — это не имена собственные каких-то частиц, а названия целых семейств. Бозоны и фермионы подчиняются квантовым статистикам Бозе-Эйнштейна и Ферми-Дирака соответственно, которые мы рассмотрим позднее. Каждая микрочастица принадлежит одному из этих двух семейств и поменять принадлежность уже не в состоянии. В теории элементарных частиц замечено, что из фермионов построено вещество, а бозоны являются переносчиками фундаментальных взаимодействий.
Если собрать вместе несколько бозонов, то они не мешают друг другу занять низшее энергетическое состояние и, следовательно, все там окажутся.
Поведение коллектива фермионов регулируется принципом Паули:
| Два одинаковых фермиона не могут находиться в одном и том же квантовом состоянии. |
В применении к атому принцип Паули запрещает двум электронам иметь одинаковый набор квантовых чисел: состояния электронов должны отличаться значением хотя бы одного из них. Если бы принципа Паули не существовало, то у всех атомов в основном состоянии все электроны находились бы на нижнем энергетическом уровне и атомы различных элементов были бы до ужаса похожи друг на друга. Таким образом, известная нам химия, все разнообразие элементов и их свойств (в частности, гамма вкусовых ощущений, отличающая, скажем, вино от сыра) - следствия принципа Паули.
До сих пор мы в основном рассматривали только атом с одним электроном. Станем добавлять лишний электрон и, соответственно, увеличивать на единицу заряд ядра. Иными словами, совершим прогулку по таблице Менделеева. Введем понятия оболочки как совокупности уровней с одинаковыми главными квантовыми числами п и подоболочки (уровни данной оболочки с одинаковыми l). Традиционные обозначения
| n= | 1 | 2 | 3 | 4 | … |
| символ | K | L | M | N | … |
Число уровней в оболочке мы фактически уже подсчитали: оно равно кратности вырождения по т и l, умноженной на 2, в соответствии с двумя возможными направлениями спина электрона. Таким образом, согласно принципу Паули, оболочка может вместить 2п2 электронов, а подоболочка - 2(2l+1) электронов (число различных значений т, удвоенное по той же причине). Итак, состояния электронов в атоме различаются квантовыми числами п, l, т и ms, и, по принципу Паули, лишь один электрон может иметь данный конкретный набор квантовых чисел.
Напомним: три квантовых числа п, l и т отражают трехмерность пространства, ms - внутренние свойства электрона.
Порядок заполнения уровней в многоэлектронных атомах определяется энергией уровней с учетом влияния заполненных оболочек. Нижние оболочки частично экранируют заряд ядра, что ведет к некулоновскому полю для высших оболочек. Этим объясняется зависимость энергии уровней от квантового числа l. Чем больше l (для электронов одной оболочки), тем дальше находится электрон от ядра и тем слабее его связь с ядром, то есть такой уровень лежит выше. При больших моментах (состояния d, l и т. д.) энергетические уровни данной оболочки близки или даже выше s -подуровней следующей оболочки. В целом заполнение идет в таком порядке (случаются небольшие отклонения):
||1s||2s, 2p||3s, 3p||4s, 3d, 4p||5s, 4d, 5p||6s, 4f, 5d, 6p|| и т.д.
В этом ряду знаком || отделены периоды таблицы Менделеева. В соответствии с полученными формулами для числа уровней в зависимости от п и l, первый период содержит 2 элемента, второй и третий - по 8, а четвертый и пятый - по 18 элементов. Здесь «вклиниваются» заполнения d -подоболочек (по 10 элементов - переходные металлы). В шестом периоде добавляется заполнение f -подоболочки ( 14 элементов - лантаниды) и т. д.
Химические свойства зависят в основном от строения внешней электронной оболочки (валентных электронов). Отсюда и вытекает периодичность повторения свойств элементов. Так, у благородных газов заполнены внешние s- и p- подоболочки из 8 электронов. У элементов первой группы (щелочные металлы) на внешней оболочке имеется всего один электрон, а галогенам ( VII группа) не хватает одного электрона для заполнения внешней p- подоболочки. Все эти рассуждения хорошо знакомы по курсу химии, но они носят качественный характер. Как известно, валентность элемента определяется не столько количеством электронов, сколько степенью легкости, с которой их можно вырвать из атома. Понятно, что внешние электроны оторвать легче, но хотелось бы получить хоть какой-нибудь количественный критерий. Таким критерием может служить потенциал ионизации, пропорциональный энергии, которую необходимо затратить, чтобы удалить электрон из атома. Расчет сложных атомов непрост, но в целом таблица Менделеева объясняется квантовой механикой. Мы ограничимся лишь самыми простыми атомами и точные расчеты заменим количественными оценками. Экспериментальные результаты представлены на рис. 5.4.
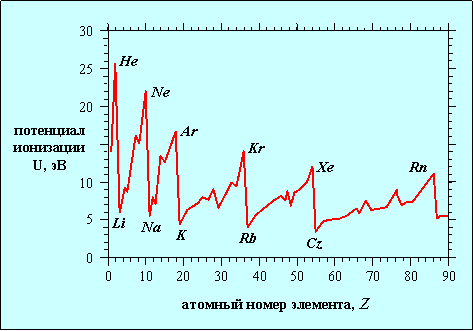
Рис. 5.4. Потенциал ионизации для элементов от водорода до урана. Ясно видна периодичность свойств элементов: пики потенциала ионизации случаются для благородных газов, минимумы - для щелочных металлов
Поиск по сайту: