Молекулы

Для простоты ограничимся рассмотрением простейших двухатомных молекул. Силы, удерживающие атомы в молекуле, вызваны взаимодействием внешних электронов, а электроны внутренних оболочек при объединении атомов в молекулы остаются в прежних состояниях. Различают два вида связи между атомами в молекуле: ионную (гетерополярную) и ковалентную (гомеополярную).

Ионная связь. Этот вид химической связи обусловлен переносом валентных электронов с одного атома на другой и кулоновским притяжением образовавшихся ионов. Иными словами, ионная связь осуществляется в том случае, когда электроны в молекуле можно разделить на две группы, каждая из которых все время находится около одного из ядер.

Электроны разделяются так, что около одного из ядер образуется избыток электронов, а около другого - их недостаток, то есть молекулу можно представить как образование, состоящее из отрицательного и положительного ионов, притягивающихся друг к другу (например, молекула NaCl состоит из ионов Na⁺ и С1^-).

Для описания ионных молекул еще до создания квантовой механики с успехом применялись полуэмпирические способы расчета энергии связи, основанные на классической электростатике. Пусть, например, мы имеем дело с молекулами типа КС1, NaCl и т. п. В начальном состоянии имеем два нейтральных атома, например К и Cl, разнесенные на бесконечно большое расстояние. Попытаемся мысленно построить из них молекулу. Затрачивая энергию Е_т, численно равную потенциалу ионизации щелочного металла, мы отрываем электрон от металла и переносим его на галоген. При присоединении электрона к последнему выделится энергия E_h (сродство галогена к электрону), так что энерговыделение на этом этапе составляет E_h-Е_т. Далее сближаем образованные нами ионы до равновесного расстояния R₀ (размер молекулы). При этом выделится дополнительная энергия кулоновского взаимодействия Е_C. Полная выделившаяся энергия и есть энергия связи Е_св получившейся молекулы: именно ее надо затратить, чтобы разорвать молекулу на составные части:

(6.1)

Учитывая, что кулоновская энергия равна

находим отсюда выражение для равновесного расстояния:

(6.2)

Применим полученную формулу для оценки размера молекулы КС1. Берем экспериментальные данные: Е_т=4.3 эВ, E_h=3.8 эВ, Е_св=4.8 эВ, так что кулоновская энергия будет

Отсюда легко находим размер молекулы

(6.3)

Получившаяся величина примерно в пять раз превышает радиус Бора и дает вполне приемлемую оценку размера молекулы.

Оценим также размер молекулы другого соединения - НС1, для которого Е_т=13.6 эВ и Е_св=2.7 эВ. Чтобы не повторять аналогичных выкладок, используем уже полученный результат. Имеем в этом случае:

что в

больше кулоновской энергии для молекулы КС1. Соответственно, размер молекулы будет в такое же число раз меньшим:

(эксперимент дает значение R₀=1.3 · 10^-10 м).

Отчуждение электрона одним ионом у другого (ионная связь) встречается в большинстве неорганических соединений, особенно в молекулах, состоящих из атомов далеких групп. Кроме соединений щелочных металлов и галогенов можно привести и другие примеры. Однако изложенные классические соображения не дают возможности вычислить независимо энергию связи молекулы (или ее размер). Само возникновение равновесного расстояния остается вне пределов компетенции такой теории. Силы электростатического притяжения между ионами должны уравновешиваться в равновесном состоянии какими-то силами отталкивания. Природа этих сил довольно сложна и связана с перекрытием оболочек ионов. При сближении атомов оболочки начинают сильно деформироваться, что препятствует дальнейшему сближению. Величина R₀ - это равновесное расстояние между ионами, на котором силы электрического притяжения уравновешиваются квантово-механическим отталкиванием атомов на близких расстояниях.

Ковалентная связь. Второй вид связи наблюдается в молекулах, где электроны, осуществляющие связь, значительную часть времени проводят в пространстве между атомами и в какой-то мере являются «общими» для обоих ядер. Гомеополярная (ковалентная) связь характерна для большинства молекул с двумя одинаковыми атомами (Н₂, N₂, 0₂ и т.д.). Гомеополярная связь не поддается классическому описанию, требует квантового рассмотрения.

Рассмотрим простейшую гомеополярную молекулу - молекулу водорода. Впервые это было

сделано в 1927 г. В. Гайтлером и Ф. Лондоном. Мы ограничимся принципиальным анализом, опуская проведение расчетов, так как нашей задачей является уяснение физической природы ковалентной (гомеополярной) связи. Схема взаимодействий в такой молекуле, состоящей из двух протонов (ядер атома водорода) А и В и двух электронов 1 и 2, показана на рис. 6.1.

Рис. 6.1. Схема взаимодействия в молекуле водорода

Уравнение Шредингера для системы имеет вид

(6.4)

где через r₁ и r₂ обозначены координаты первого и второго электронов, а Н - гамильтониан системы:

(6.5)

Гамильтониан Н₁ содержит оператор кинетической энергии электрона и потенциальную энергию того же электрона в кулоновском поле ядра А. Аналогичную структуру имеет гамильтониан Н₂. Оператор U описывает четыре взаимодействия: электрона 1 с ядром В, электрона 2 с ядром А, электронов между собой и ядер - также между собой. Ядра имеют массу, примерно в 2 000 раз превышающую массу электрона, поэтому они движутся гораздо медленнее электронов, и в первом приближении их можно считать неподвижными (такое приближение называется адиабатическим). Поэтому волновая функция

рассматривается как функция координат только электронов, а расстояние R между ядрами, важное в проблеме ковалентной связи, входит в волновую функцию y как параметр. Получающиеся из уравнения Шредингера собственные значения энергии будут тогда зависеть от расстояния R, то есть

причем в случаях параллельной и антипараллельной ориентации спинов электронов характер этой зависимости оказывается различным.

Полная волновая функция зависит не только от пространственных координат электронов, но и от их спинов. Вследствие принципа Паули (согласно которому данный набор квантовых чисел может иметь лишь одна частица), такая полная волновая функция должна быть антисимметричной относительно перестановки электронов. Поскольку спиновое состояние не зависит от орбитального, пространственные и спиновые переменные разделяются, и полную волновую функцию электронов в молекуле водорода можно представить в виде произведения координатной и спиновой функций:

(6.6)

Из принципа Паули следуют свойства волновых функций:

Симметричная спиновая волновая функция соответствует параллельному расположению векторов спинов электронов, то есть суммарному спину электронов S=1. Такое состояние называется триплетным по числу (2S+1)=3 возможных проекций суммарного спина. Во втором же случае антисимметричная спиновая функция связана с противоположно ориентированными спинами, дающими в сумме S=0, и, следовательно, возможно только одно значение проекции полного спина, и состояние называется синглетным.

Взаимодействие между нейтральными атомами, когда расстояние между ядрами R много больше характерных размеров электронных оболочек, то есть радиуса Бора

практически отсутствует, а энергия системы равна удвоенной энергии связи атома водорода 2Е₀, где

При уменьшении R до нуля эта энергия будет бесконечно возрастать из-за кулоновского отталкивания ядер.

Результаты расчетов можно описать следующим образом. Если спины электронов параллельны, то при сближении атомов водорода энергия системы монотонно увеличивается, никакого связанного состояния не возникает (кривая Е₊ на рис. 6.2).

Рис. 6.2. Зависимость энергии Е молекулы водорода от расстояния R между атомами: на больших расстояниях существуют два нейтральных атома водорода с общей энергией 2Е₀=2(-13.6 эВ)=-27.2 эВ; кривая Е_- соответствует триплетному состоянию электронов и проходит выше асимптотического значения 2Е₍₎ — связанного состояния молекулы в этом случае не существует; кривая Е₊ соответствует синглетному состоянию электронов, она имеет минимум при R=R₀ (конечный размер молекулы), расстояние которого от асимптотического значения и есть энергия связи Е_св молекулы водорода

В этом случае предоставленные самим себе два атома вновь разойдутся, стремясь к состоянию с наименьшей возможной энергией. Условие существования связанного состояния - наличие минимума энергии системы при некотором значении R₀ - выполняется только при синглетном состоянии электронов, когда их спины антипараллельны (кривая Е₊ на рис. 6.2).

Понять такое поведение энергии можно на качественном уровне, если рассмотреть два водородных атома, находящихся на большом расстоянии

друг от друга. Тогда оператором взаимодействия U в гамильтониане (6.5) можно пренебречь, и мы имеем два независимых атома, описываемых суммой гамильтонианов Н₁ и Н₂. Решения соответствующего каждому из них уравнения Шредингера мы уже знаем. Введем обозначения для получающихся волновых функций: y_A( r ₁) и y_В( r ₂). Тогда решение для суммы гамильтонианов Н₁+Н₂ будет представляться в виде произведения волновых функций

а энергия - в виде суммы энергий, то есть будет равна 2Е₀. Физический смысл произведения волновых функций очевиден: электрон 1 находится в поле ядра А, а электрон 2 - в поле ядра В. Но электроны неразличимы, и эта физическая ситуация ничем не отличается от случая, когда электрон 2 находится в поле ядра А, а электрон 1 - в поле ядра В. Этому соответствует иное произведение волновых функций:

которое тоже является решением уравнения Шредингера с той же энергией 2Е₀. Согласно принципу суперпозиции, решением с этой же энергией будет и любая линейная комбинация указанных произведений. Поскольку принцип Паули требует, чтобы полная волновая функция была либо симметрична, либо антисимметрична по пространственным координатам электрона, она должна иметь вид

(6.7)

где N₊ - вычисляемые нормировочные коэффициенты, обеспечивающие равенство единице полной вероятности:

Подставляя сюда выражения (6.7) и учитывая, что y_A( r ) и y_В( r ) уже нормированы на единицу, получаем

(6.8)

откуда

(6.9)

Величина Р, называемая интегралом перекрытия, равна

(6.10)

Она характеризует степень перекрытия волновых функций y_A и y_В, то есть степень независимости пространственного распределения электронов друг от друга, и играет важную роль в теоретических расчетах свойств молекул.

Если учесть теперь оператор взаимодействия U, то в зависимости от симметрии волновой функции y ₊ получатся поправки к энергии разных знаков. В случае антисимметричного состояния y_- (полный спин электронов S=1) поправка получается положительной (отталкивание атомов), и связанного состояния не возникает. В случае же симметричного состояния y₊ (полный спин электронов S=0) поправка для больших R отрицательна (притяжение атомов), что приводит к образованию молекулы водорода.

Осмыслить такое поведение поправки к энергии помогает график волновой функции. Ось z направим по линии, соединяющей ядра атомов водорода, а начало отсчета выберем в средней точке между ядрами, так что координаты ядра А равны (0, 0, -R/2), а ядра В - (0, 0, R/2). Для простоты рассмотрим волновые функции на этой оси, причем для случая симметричного расположения электронов относительно начала отсчета:

Тогда

(6.11)

Графики этих функций представлены на рис. 6.3.

Рис. 6.3. Волновые функции электронов в молекуле водорода на оси, соединяющей ядра атомов, для синглетного y₊ и триплетного y_- состояний

Мы видим, что в обоих случаях существует наибольшая вероятность найти электроны вблизи ядер - волновые функции имеют экстремумы в точках

Однако при сближении атомов в пространстве между ядрами происходит перераспределение плотности электронов, поведение которой различается в зависимости от типа симметрии пространственной части волновой функции - y₊ или y_-. В состоянии y₊ электроны часть времени проводят в области между протонами (волновая функция в этой области заметно отлична от нуля). В центре между атомами получается электронное облачко, притягивающее к себе протоны - возникает стягивающее действие и образуется молекула. В состоянии же y_- плотность электронов между протонами уменьшается (волновая функция проходит через нуль), отталкивание протонов не экранируется, что и приводит к увеличению энергии системы в этом состоянии (см. рис. 6.2). Положение минимума, таким образом, определяется из решения уравнения Шредингера с учетом потенциальной энергии электрического взаимодействия электронов и протонов в молекуле.

Численные результаты R₀=0.87 · 10^-10 м, Е_св=3.1 эВ для кривой Е₊, полученные в таком подходе, следует сравнить с экспериментальными данными: R₀=0.74 · 10^-10 м, Е_св=4.5 эВ. Разница в энергии связи составляет 31%, в размере молекулы - 17%.

Комбинации различных типов связи. Мы познакомились с двумя типами связи - ионной и ковалентной. В первой основную роль играет «перескок» электронов от одного атома к другому, во второй - дополнительные силы притяжения между атомами, порождаемые парой электронов с противоположными спинами. На самом деле оказывается, что такое резкое разделение не есть внутреннее свойство системы, но, скорее, недостаток наших методов расчета. Так, для улучшения согласия с экспериментом использованное приближение Гайтлера-Лондона может быть уточнено. Именно, ранее исходным моментом были волновые функции электронов - электрона 1 в поле ядра А и электрона 2 - в поле ядра В. Но электрон 1 также находится и в поле ядра В, а электрон 2 - в поле ядра А. Эти взаимодействия были учтены в поправочных членах, входящих в оператор U. Можно, однако, попытаться включить эти взаимодействия в рассмотрение с самого начала. Для этого представим волновую функцию первого электрона в виде

(6.12)

где Р - тот же интеграл перекрытия (6.10). Аналогичный вид имеет и волновая функция второго электрона:

Волновую функцию синглетного двухэлектронного состояния строим как произведение

(6.13)

Мы видим, что здесь содержится волновая функция Гайтлера-Лондона - это последнее слагаемое в (6.13). Однако в приведенных формулах содержится и описание другого случая: это слагаемые

Физический смысл первого из них достаточно очевиден: оба электрона сосредоточены вокруг ядра А, образуя ион водорода Н ^-, в то время как ядро В, лишившееся электрона, образует ион Н⁺. Мы видим, что этот случай описывает ионную связь. Второе слагаемое описывает аналогичную ситуацию, только ядра A и В меняются ролями. Для симметричной молекулы при обмене ядер местами ничего не меняется, откуда следует равенство коэффициентов

Таким образом, волновая функция (6.11) описывает некую комбинацию ионной и ковалентной связи, причем относительные веса этих двух типов связи одинаковы. Физически это, однако, не так, поскольку мы уже убедились, что метод Гайтлера-Лондона дает неплохое описание молекулы водорода. Но мы нащупали путь. Ясно, что недостаток метода Гайтлера-Лондона заключается в пренебрежении ионными членами, а недостаток только что изложенного подхода (его называют методом молекулярных орбит) - в переоценке влияния этих членов.

Можно принять оба этих метода как два различных исходных приближения, и естественным обобщением может стать улучшение численных значений коэффициентов в волновой функции, определяющих статистический вес ионной и ковалентной связей. Представим, например, симметричную волновую функцию как суперпозицию отдельных двухэлектронных состояний с произвольными коэффициентами а₁, а₂, а₃:

(6.14)

При использовании такой волновой функции согласие с экспериментом заметно улучшается. В реальных расчетах коэффициенты а₁, а₂, а₃ определяются из условия минимума средней энергии, и их численные значения получаются автоматически, в зависимости от свойств системы. Если окажется, что численное значение одного из них намного превосходит по абсолютной величине два других, то можно говорить о преобладании связи определенного типа.

Так, если

то это будет ионная связь А^-В⁺ (электрон «перепрыгнул» с ядра В на ядро А).

Е сли

то это случай ионной связи А⁺В^- (электрон перешел с ядра А на ядро В).

Если же, наконец,

то мы имеем дело с ковалентной связью.

Этот подход применим как к молекулам из двух разных атомов, так и к соединениям одинаковых атомов, и позволяет учесть вклад ковалентного соединения в ионных молекулах и вклад ионной связи - в ковалентных молекулах. В применении к симметричным молекулам должно выполняться равенство

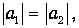
но третий коэффициент а₃ остается независимым, в отличие от метода молекулярных орбит. Сравнение экспериментов с расчетами по волновой функции (6.14) показало, что доля ионной связи в ковалентной молекуле атома водорода равна 20 %.

Поиск по сайту: