АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Столкновение молекул. Эффективное сечение молекулы. Число столкновений молекулы в единицу времени. Длина свободного пробега молекулы

Читайте также:
  1. A) эффективное распределение ресурсов
  2. I. Россия в период правления Бориса Годунова (1598-1605). Начало Смутного времени.
  3. I. Россия в период правления Бориса Годунова (1598-1605). Начало Смутного времени.
  4. Ni – число абонентских номеров для i- ой ТС.
  5. Атомная масса и атомное число.
  6. АУТОДАФЕ И ЧИСЛО ЖЕРТВ
  7. Билет 30. Понятие «Нового времени», Проблемы периодизации истории Нового времени.
  8. Билет №19. Правление Федора Иоанновича. Начало Смутного времени.
  9. В XVII веке Хотмыжск входил как центр уезда в такую военно-административную единицу как Белгородский полк.
  10. В журнале движения больных отделения отмечаются сведения о движении больных: число выбывших и поступивших.
  11. Векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.
  12. Випадкові події і величини, їх числові характеристики

Молекулы газа, находясь в хаотическом движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, называемым длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с очень большим числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул < l >.

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 1). Он зависит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры).


 

Рис.1

 

Так как за 1 с молекула в среднем проходит путь, который равен средней арифметической скорости <v>, и если < z > — среднее число столкновений, которые одна молекула газа делает за 1 с, то средняя длина свободного пробега будет

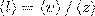
Для определения < z > представим себе молекулу в виде шарика диаметром d, которая движется среди других как бы застывших молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри так называемого ломаного цилиндра радиусом d (рис. 2).

Среднее число столкновений за 1 с равно числу молекул в объеме, так называемого ломаного цилиндра:

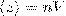
где n — концентрация молекул, V = πd2<v>,где <v> — средняя скорость молекулы или путь, пройденным ею за 1 с). Таким образом, среднее число столкновений

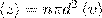
Расчеты показывают, что при учете движения других молекул

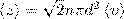
Тогда средняя длина свободного пробега

т. е. < l > обратно пропорциональна концентрации n молекул. С другой стороны, p=nkt. Значит,



1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)