Частные случаи первого закона термодинамики для изопроцессов

Хотя и редко показываемая, многосторонность Циклопа в использовании своих способностей весьма поразительна. Ниже приведён список впечатляющих подвигов, достигнутых Циклопом (с номерами выпусков для проверки).

· Uncanny X-Men #124: Находясь в ловушке в Мире убийства (контролируемом злодеем Аркадой), Циклоп спас Ночного Змея, очистив комнату от атакующих роботов одним только выстрелом, который отражался от врага до врага, в итоге уничтожив в общей сложности восемь нападающих.

· Uncanny X-Men #144: Играя в пул, он использовал один точный оптический выстрел для удара по киевому шару, загнав в лузу каждый шар на столе.

· Uncanny X-Men #152: Он отразил свой выстрел от трёх поверхностей, чтобы поразить Себастьяна Шоу и толкнул его к поджидающему Колоссу. Это показывает впечатляющий уровень ума (учитывая силу Шоу поглощать кинетическую энергию), чтобы приспособить его стратегию таким образом.

· Uncanny X-Men #170: Пытаясь объяснить своё мутанство Мадлен Прайер, он подбросил монету и прострелил её центр, оставив внешнюю сторону нетронутой.

· Uncanny X-Men #175: Когда Люди Икс были загипнотизированы думать, что Циклоп — Тёмный Феникс, они попытались преследовать его. ПобедивКолосса, Ночного Змея и Грозу в быстрой последовательности, он помчался в Опасную Комнату. Внутри он создал пейзаж джунглей, чтобы спрятаться в нём от других Людей Икс. Они пытались его преследовать, но он перехитрил их, победив Призрачную Кошку, Росомаху, Колосса, Грозу и Шельму, всё это время страдая от сломанных рёбер.

· X-Men (том 2) #112: Во время внедрения на Дженошу с Росомахой, он сделал выстрел, отразив его от двух углов, чтобы вывести из строя двух поджидающих врагов. Росомаха позже заметил, что тогда он впервые видел, как Циклоп «рисовался». В том же комиксе он и Росомаха оказались против нескольких вооружённых охранников. Циклоп использовал несколько маленьких выстрелов, чтобы повредить оружие каждого из врагов, прежде чем те сделали хоть выстрел. В более позднем выпуске этой истории в сражении с Магнитом он выстрелил мимо Магнита (которым только что пробил стену), попав в упавший шлем Магнита, который отскочил и ударил последнего в голову. Наконец, хотя это не было показано, Росомаха рассказал, что помнит, как Циклоп открыл замок машины, используя только свои выстрелы.

· New X-Men #137: Во время сюжета 'Бунт у Ксавье' он — один из Людей Икс, померившихся силами с Омега Бандой Квентина Квайра. КогдаКрасношеий бросил ему вызов, он сделал один выстрел, достаточно точный, чтобы сломать Красношеему нос, не причинив других повреждений. В последующем бою он (при делании колеса) выстрелил второй раз, сломав ногу Радиану.

· Два примера степени его силы было показано в выпусках Uncanny X-Men и Astonishing X-Men. В Uncanny X-Men #336, сражаясь со злым существом, известным как Натиск, Циклоп снял свой прибор видения, выпустив огромный выстрел, который пробил дыру в броне Натиска. Затем в Astonishing X-Men #8 при нападении на Институт Ксавье повреждённого Стража Циклоп вновь снял прибор, высвободив выстрел, отбросивший Стража через лужайку и полностью сравнявший с землёй большую часть леса перед ним. После этого Росомаха констатировал, что только что выпущенный выстрел был одной из причин, по которым Циклоп так долго являлся лидером Людей Икс.

· Civil War: X-Men. В #3 он стрелял в Епископа, перегрузив его энергией, а в #4, пытаясь пробить укреплённую дверь, заряжал его, и Железный человекоценил энергию почти в два гигаватта. Два гигаватта это эквивалент выпуска большого ядерного реактора.

· В X-Factor #68 в бою против Апокалипсиса, Циклоп, каким-то образом усиленный его женой и сыном, выпустил необычайно большой оптический выстрел, который победил Апокалипсиса. Это проявление похоже на временами демонстрируемое Циклопом при снятии прибора видения.

· В X-Factor #25, зная, что его выстрел отрикошетил бы от брони механической лошади Войны, Циклоп сам отскочил от статуи на кладбище, чтобы добраться до коня Войны, и сделал оптический выстрел прямо в рот, уничтожив лошадь и показав впечатляющую ловкость и тактическую способность.

· В X-Factor #14 Циклоп столкнулся с Форммастером, искавшим Двенадцать. Воспользовавшись тем, что поле боя находилось возле завода по очистке нефти, и провоцируя Форммастера, он заставил робота выстрелить в нефтяные цистерны, устроив взрыв, в то время как сам Циклоп использовал оптический выстрел для создания траншеи и закрылся отстреленной им одной из рук Форммастера.

· В Astonishing X-Men #23 когда он был в плену у Лорда власти Крууна, диктатор сообщил Циклопу: «Даже проклятый Колосс не может прорваться сквозь наши тюремные стены». С лёгкостью, обманом убедив Крууна, что он лишился сил, Циклоп отправил Крууна в нокаут прямым выстрелом в лицо и снёс большую часть внешней структуры тюрьмы, которую Круун нахваливал ранее. Находившийся несколькими уровнями выше Скотта Росомаха был освобождён восходящим лучом, который разбил наручники. Тот же луч он использовал как сигнал остальным Людям-X найти тюрьму — всё это будучи недавно воскрешённым и после пыток.

Идеальный газ. Основное уравнение мкт. Молякулярно-кинетическое толкование абсолютной температуры. Уравнение Менделеева-Клайперона. Законы идеальных газов. Число степеней свободы молекул. Средняя энергия молекул.

ьс

Тогда давление газа, оказываемое им на стенку сосуда,

(1)

Если газ в объеме V содержит N молекул, движущихся со скоростями v₁, v₂,..., v_N, то целесообразно рассматривать среднюю квадратичную скорость

(2)

которая характеризует всю совокупность молекул газа. Уравнение (1) с учетом (2) примет вид

(3)

Выражение (3) называется основным уравнением молекулярно-кинетической теории идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.

Учитывая, что n = N / V, получим

(4)

или

(5)

где Е — суммарная кинетическая энергия поступательного движения всех молекул газа.

Так как масса газа m=Nm₀, то уравнение (4) можно переписать в виде

Для одного моля газа m=М (М — молярная масса), поэтому

где V_m — молярный объем. С другой стороны, по уравнению Менделеева-Клапейрона, pV_m=RT. Таким образом,

откуда

(6)

Так как M=m₀N_A, где m₀ — масса одной молекулы, a N_A — постоянная Авогадро, то из уравнения (6) следует, что

(7)

где k=R/N_A — постоянная Больцмана. что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водорода — 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с.

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа

(8)

(использовали формулы (5) и (7)) прямо пропорциональна термодинамической температуре и зависит только от нее. Из этого уравнения видно, что при Т=0 <ε₀>=0, т. е. при 0 К прекращается поступательное движение молекул газа, а значит, его давление равно нулю. Таким образом, термодинамическая температура есть мера средней кинетической энергии поступательного движения молекул идеального газа, и формула (8) раскрывает молекулярно-кинетическое толкование температуры.

Физическое состояние массы газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, задаваемая в общем виде дается выражением

где каждая из переменных является функцией двух других.

Французский инженер и физик Б. Клапейрон (1799—1864) получил уравнение состояния идеального газа, объединив законы Бойля—Мариотта и Гей-Люссака. Пусть данная масса газа занимает объем V₁, образует давление р₁ и находится при температуре T₁. В другом произвольном состоянии масса газа описывается параметрами р₂, V₂, T₂ (рис. 1). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1–1'), 2) изохорного (изохора 1'–2).

Рис.1

В соответствии с законами Бойля — Мариотта и Гей-Люссака запишем:

(1)

(2)

Исключив из уравнений (1) и (2) получим

Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина pV/T остается постоянной, т. е.

(3)

Выражение (3) является уравнением Клапейрона, в котором В — газовая постоянная, которая различна для разных газов.

Русский ученый Д. И. Менделеев (1834—1907) сопоставил уравнение Клапейрона с законом Авогадро, отнеся уравнение (3) к одному молю, использовав молярный объем V_m. По закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем V_m, поэтому постоянная В будет равной для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению

(4)

удовлетворяет только идеальный газ, и оно является уравнением состояния идеального газа, которая называется также уравнением Менделеева-Клайперона.

Числовое значение молярной газовой постоянной найдем из формулы (4), считая, что моль газа находится при нормальных условиях (р₀= 1,013•10⁵ Па, T₀=273,15 К, V_m=22,41•10^-3 м³/моль): R=8,31 Дж/(моль•К).

От уравнения (4) для моля газа можно перейти к уравнению Менделеева-Клапейрона для произвольной массы газа. Если при данных давлении и температуре один моль газа занимает молярный объем V_m, то при тех же условиях масса m газа займет объем V= (m/М)V_m, где М — молярная масса (масса одного моля газа). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы m газа

(5)

где ν = m/M — количество вещества.

Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана: k=R/N_A=1,38•10^-23 Дж/К

Исходя из этого уравнение состояния (4) запишем в виде

где N_A/V_m = n — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения

(6)

мы видим, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых давлении и температуре любой газ содержат в единице объема одинаковое число молекул. Число молекул, которые содержатся в 1 м³ газа при нормальных условиях, называется числом Лошмидта: N_L = p₀/(kT₀) = 2,68•10²⁵ м^-3

Термодинамические параметры. Равновесные состояния и процессы. Внутренняя энергия идеального газа. Работа газа при изменении его объема. Количество теплоты. Первый закон термодинамики.

Термодинамическими величинами называют физические величины, применяемые при описании состояний и процессов в термодинамических системах.

Термодинамика рассматривает эти величины как некоторые макроскопические параметры и функции, присущие системе, но не связанные с её микроскопическим устройством. Вопросы микроскопического устройства изучает статистическая физика.

Функции состояния

Функции состояния зависят только от текущего состояния системы и не зависят от пути, по которому система пришла в это состояние.

Функции состояния в термодинамике включают:

· температуру,

· давление,

· объём,

· энтропию,

а также термодинамические потенциалы.

В зависимости от выбранной модели некоторые из этих величин, строго говоря, могут быть не функциями, а независимыми переменными.

Эти величины не являются независимыми. Связь между термодинамическими параметрами для конкретной системы называется уравнением состояния.

В случае, если известно каноническое уравнение состояния, задание любой пары параметров из следующих:

· энтропия и объём,

· энтропия и давление,

· температура и объём,

· температура и давление,

позволяет вычислить остальные два параметра.

Функции процесса

Функции процесса зависят не только от текущего состояния системы, но также и от пути, по которому система пришла в данное состояние.

Функции процесса в термодинамике включают:

· количество теплоты и

· термодинамическую работу.

Эти величины, однако, могут быть «превращены» в функции состояния с помощью интегрирующего множителя:

· , где (энтропия) — функция состояния.

· , где (давление) и (объём) — функции состояния.

Для вычисления внутренней энергии одноатомного идеального газа необходимо среднекинетическую энергию движения одного атома умножить на число атомов в рассматриваемом объеме.

Число атомов N, в свою очередь, может быть выражено через число Авогадро N _A и количество вещества n = m / M.

Произведение двух постоянных величин – постоянной Больцмана и числа Авогадро равно универсальной газовой постоянной:

Таким образом, после ряда преобразований получаем, что, для одноатомного идеального газа внутренняя энергия прямо пропорциональна его абсолютной температуре, массе, и обратно пропорциональна молярной массе. Так как газ одноатомный, коэффициент пропорциональности между этими величинами равен 3/2.

Изменение внутренней энергии одноатомного идеального газа при переходе из одного состояния в другое будет равно:

Существенно, что изменение этой величины при переходе газа из состояния с температурой Т ₁ в состояние с температурой Т ₂определяется только его начальным и конечным состоянием и не зависит от способа перехода из одного состояния в другое.

Q - энергия, которую тело теряет или приобретает при передаче тепла.
Формула количества теплоты зависит от протекающего процесса.

Формулы количества теплоты при некоторых процессах:

Количество теплоты при нагревании и охлаждении.

Количество теплоты при плавлении или кристаллизации.

Количество теплоты при кипении, испарении жидкости и конденсации пара.

Количество теплоты при сгорании топлива.

Количество теплоты всегда передается о т более горячих тел к более холодным до достижения ими одинаковой температуры (теплового равновесия), если нет иных процессов, кроме теплопередачи.
В замкнутой системе тел выполняется уравнение теплового балланса: Q₁+ Q₂+... = 0 - количество теплоты, которое теряют горячие тела, равно количеству тепла, получаемому холодными.

Полезные формулы:

Количество теплоты, переданное телу,
идет на изменение его внутренней энергии
и на совершение им работы (Первый закон термодинамики).

Закон Джоуля-Ленца: в неподвижном металлическом проводнике вся энергия электрического тока превращается в тепло:

- закон Джоуля - Ленца.

Первый закон термодинамики (закон сохранения энергии для тепловых процессов) определяет количественное соотношение между изменением внутренней энергии системы дельта U, количеством теплоты Q, подведенным к ней, и суммарной работой внешних сил A, действующих на систему.

Первый закон термодинамики - Изменение внутренней энергии системы при ее переходе из одного состояния в другое равно сумме количества теплоты, подведенного к системе извне, и работы внешних сил, действующих на нее:

Первый закон термодинамики - количество теплоты, подведенное к системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами:

Частные случаи первого закона термодинамики для изопроцессов

При изохорном процессе объем газа остается постоянным, поэтому газ не совершает работу. Изменение внутренней энергии газа происходит благодаря теплообмену с окружающими телами:

При изотермическом процессе количество теплоты, переданное газу от нагревателя, полностью расходуется на совершение работы:

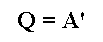
При изобарном расширении газа подведенное к нему количество теплоты расходуется как на увеличение его внутренней энергии и на совершение работы газом:

Адиабатный процесс - термодинамический процесс в теплоизолированной системе.

Теплоизолированная система - система, не обменивающаяся энергией с окружающими телами.

Формула КПД теплового двигателя:

Здесь Q₁ - количество теплоты, полученное рабочим телом,
Q₂ - количество теплоты, отданное холодильнику.
A - полезная работа.

Формула Карно для оценки максимального КПД теплового двигателя:

Поиск по сайту: