 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Спин электрона и тонкая структура спектров
Дальнейшее исследование атомных спектров показало, что многие спектральные линии имеют два близких компонента. Так, еще в 1887 г. А. Майкельсон обнаружил расщепление a -линии серии Бальмера в водороде, порождаемой переходом

Она оказалась состоящей из двух линий со средней длиной волны 6 563 A.
| Ангстрем (A) - используемая в атомной физике внесистемная единица длины 1 A=10-10 м. |
Разность длин волн равна 0.14 A (то есть относительная величина расщепления порядка 10-5). Были обнаружены и линии, расщепленные на 3, 4 и более компонентов. Расщепление линий, как мы теперь понимаем, означает расщепление энергетических уровней атома: у них появляется, как говорят, тонкая структура. Значит, существует неучтенное взаимодействие. Мы говорили, что расщепление линий возникает, например, когда наложенное внешнее поле нарушает симметрию системы. А здесь неучтенное взаимодействие проявляется в отсутствие внешних полей, то есть оно должно быть связано с какими-то внутренними свойствами атома.
Оказалось, что это действительно проявление внутренних свойств, но не атома в целом, а электрона. В 1925 г. С. Гаудсмит и Дж. Уленбек выдвинули гипотезу спина электрона: они предположили существование у электрона собственного момента импульса, не связанного с орбитальным движением. Сначала спин представляли себе как верчение (англ. spin) электрона вокруг собственной оси (аналог суточного вращения Земли). Потом осознали, что «верчение» нельзя понимать буквально: численные оценки давали линейную скорость верчения, превышающую скорость света.
| Под спином понимается собственный момент количества движения электрона как врожденное квантовое свойство. |
Его существование остается загадкой, если находиться только в рамках квантовой механики Гейзенберга - Шредингера. Естественное объяснение спин получил только в релятивистской квантовой теории П. Дирака, соединившей теорию относительности с квантовой механикой.
Из опытов следовало, что электрону надо приписать спиновое квантовое число s=1/2, имеющее те же свойства (см. формулу (5.5)), что и квантовое число l. (Принято для краткости спиновое квантовое число для краткости называть спином. В дальнейшем мы тоже будем использовать эту терминологию).
Соответственно, существует единственное собственное значение оператора квадрата спина

а проекция спина на какую-то ось (пробегая через единицу h все значения от максимального до минимального) записывается в виде

где ms принимает лишь два значения

Число ms называют магнитным спиновым квантовым числом.
Откуда же взялось расщепление спектральных линий? Попытаемся понять это с помощью полуклассических рассуждений. В классической физике любое вращение электрического заряда создает магнитное поле. Вращающийся по орбите радиусом R классический электрон можно представить как виток с током силой l, охватывающий площадь pR2, то есть как магнитный диполь с магнитным моментом

(Эту формулу знал еще Ш. Кулон).
Классическая оценка: электрон на орбите радиусом R и скоростью v имеет период обращения

Возьмем какую-нибудь точку на орбите. За время Т через нее проходит заряд е, то есть сила тока по определению равна
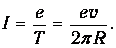
Кроме того, электрон имеет орбитальный момент

так что ток можно выразить через орбитальный момент, исключив скорость электрона:
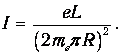
Тогда орбитальный магнитный момент, создаваемый электроном, равен
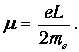
Заменим теперь в соответствии с правилами квантования

и получим выражение для орбитального магнитного момента, которое может быть выведено и более строго:
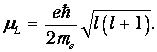
| (5.11) |
Отсюда следуют выводы:
· Естественная единица для магнитных моментов в микромире - так называемый магнетон Бора
· Проекция магнитного момента на любую ось всегда должна быть целым кратным магнетона Бора: (Теперь понятно, почему квантовое число т названо магнитным.) · Отношение орбитального магнитного момента электрона к его орбитальному моменту импульса, называемое гиромагнитным отношением, равно |
Эксперименты показали, что спин электрона обладает двойным магнетизмом: собственный магнитный момент электрона, связанный со спином, равен
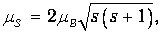
то есть гиромагнитное отношение для него оказалось в два раза большим (е/те). Это - лишнее доказательство того, что электрон нельзя представлять себе как заряженный шарик, вращающийся вокруг собственной оси: в таком случае должно было бы получиться обычное гиромагнитное отношение. Для проекции собственного магнитного момента имеем

и поскольку

то

В итоге для проекции спинового магнитного момента снова получились целые кратные магнетона Бора, как и для орбитального движения. По какой-то причине природа предпочитает иметь дело с целым магнетоном Бора, а не с его частями. Поэтому полуцелое значение собственного момента количества движения она компенсирует двойным гиромагнитным отношением.
Теперь можно понять, почему наличие у электрона собственного магнитного момента приводит к появлению какого-то неучтенного до сих пор взаимодействия. Для этого опять перейдем на полуклассический язык. Орбитальное движение электрона создает магнитное поле, которое действует на собственный магнитный момент электрона. Подобным образом магнитное поле Земли воздействует на стрелку компаса. Энергия этого взаимодействия сдвигает энергетические уровни атома, причем величина сдвига зависит, вообще говоря, от спинового и орбитального моментов количества движения.
Важный вывод:
| Взаимодействие спинового и орбитального магнитных моментов приводит к снятию вырождения и к расщеплению спектральных линий. |
Пример 1. Оценим расщепление уровней энергии вследствие взаимодействия спинового и орбитального магнитного моментов электрона в атоме водорода.
Круговой виток радиусом R с током силой I порождает в центре магнитное поле

В этой главе было показано, что вращающийся по орбите электрон можно представить как виток с током

Здесь для оценки мы положили

Тогда получаем для магнитного поля, создаваемого орбитальным движением электрона в атоме, величину порядка

Энергия взаимодействия собственного магнитного момента электрона с этим магнитным полем равна по порядку величины

Для оценки положим R равным боровскому радиусу первой орбиты аB. Подставляя сюда выражения для аB и mB и учитывая, что

получаем оценку сдвига энергетических уровней

| (5.13) |
где a - введенная выше постоянная тонкой структуры. Энергия первого уровня атома водорода, как известно, равна

так что (3.13) можно переписать как

Поскольку

a E=13.6 эВ, то
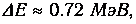
а относительный сдвиг уровней

что соответствует экспериментальным данным.
Это и есть оценка (не расчет) искомого расщепления уровней. В сущности, расщепление уровней - это релятивистский эффект: по Бору скорость электрона на первой орбите

и

Поэтому не удивительно, что до конца свойства спина могут быть поняты только в релятивистской квантовой теории. Мы не ставим себе такую задачу, но просто будем учитывать наличие у электрона этого удивительного свойства.
Экспериментальное доказательство существования спина электрона было дано в опыте Штерна-Герлаха в 1922 г. Идея опыта состоит в том, что в магнитном поле, неоднородном по оси z, на электроны действует смещающая сила, направленная вдоль поля. Происхождение этой силы проще уяснить сначала на примере электрического диполя, помещенного в электрическое поле. Электрический диполь представляет собой пару противоположных зарядов + е, расположенных на малом расстоянии l друг от друга. Величина электрического дипольного момента определяется как

причем вектор l считается направленным от отрицательного заряда к положительному.
Пусть положительный заряд находится в точке r, а отрицательный - в точке r 1, так что

Пусть диполь помещен в электрическое поле с напряженностью Е ( r ). Найдем силу, действующую на диполь. На положительный заряд действует сила

на отрицательный -
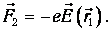
Результирующая сила будет

Так как расстояние между зарядами мало, то поле в точке расположения отрицательного заряда можно приближенно записать как

Подставляя это разложение в выражение для силы F, находим

| (5.14) |
Если поле однородно (Е не зависит от r), то на заряды диполя действуют равные и противоположно направленные силы и результирующая сила равна нулю, как и следует из уравнения (5.14). Как известно, такая пара сил не смещает диполь (который в целом электрически нейтрален), но лишь поворачивает его вдоль поля (магнитный аналог - стрелка компаса). В неоднородном же поле результирующая сила отлична от нуля. В частном случае, когда поле Е зависит только от координаты z, в уравнении (5.14) отлична от нуля лишь производная по z
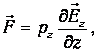
| (5.15) |
где Ez - проекция электрического момента на ось z. Неоднородное поле стремится втянуть диполь в область, где оно сильнее.
Магнитных зарядов не существует, но магнитный диполь реализуется витком с током, и его свойства аналогичны свойствам электрического диполя. Поэтому в формуле (5.15) надо заменить электрическое поле на магнитное, электрический момент - на магнитный и написать для силы, действующей на электрон в опыте Штерна-Герлаха, аналогичное выражение

Схема опыта: пучок атомов пролетает сквозь неоднородное магнитное поле, направленное поперечно к скорости атомов. Сила, действующая на магнитные моменты атомов, отклоняет их. Соответственно возможным значениям проекции магнитного момента на направление поля первоначальный пучок расщепляется на несколько пучков. Если полный магнитный момент атома определяется только спином электрона, то первоначальный пучок расщепится на два. Для многоэлектронных атомов расщепленных пучков может быть больше. Для своего эксперимента Штерн и Герлах использовали серебро, которое испарялось в электрической печке. Численные значения расщепления составляли доли миллиметра. Авторы подчеркнули в своих выводах, что неотклоненных атомов не было зарегистрировано. Ниже мы увидим, что это - специфика опытов с элементами первой группы.
Главный результат опытов Штерна и Герлаха - прямое экспериментальное доказательство квантования направления магнитного момента атомов. Согласно классической физике, первоначальный пучок должен не расщепиться, а размазаться в соответствии с произвольностью проекции магнитного момента на направление магнитного поля. Соответственно, на экране за прибором вместо двух раздельных линий, оставленных атомами серебра, должна была бы наблюдаться размытая полоска.
Пример 2. Узкий пучок атомов со скоростью v и массой т пропускается через поперечное неоднородное магнитное поле, в котором на них действует сила Fz (рис. 5.3). Протяженность области поля l1, расстояние от магнита до экрана l2. Определим угол отклонения q следа пучка атомов на экране от его положения при выключенном магнитном поле.

Рис. 5.3. Отклонение атомов магнитным полем
Здесь мы имеем дело с задачей классической механики, которая позволяет подготовиться к количественному рассмотрению опыта Штерна-Герлаха. Время пролета атома через магнит равно

Все это время на атом действует поперечная сила Fz, придающая ему поперечное ускорение

За время пролета атом отклонится на расстояние

и приобретет поперечную скорость

Это значит, что из магнита атом вылетает под углом q к первоначальному направлению движения, причем
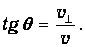
Следовательно, при пролете расстояния l2 до экрана атом отклонится еще и на расстояние

Складывая отклонения s1 и s2, получаем искомое отклонение следа атома на экране

| (5.16) |
Часто в задаче стоит вопрос об отклонении пучка атомов при выходе из магнита. В таком случае надо положить l2=0 в полученной формуле (5.16).
Пример 3. Узкий пучок атомов серебра при прохождении магнитного поля с неоднородностью

протяженностью l1=4 см расщепился на два пучка. Экран для наблюдения установлен на расстоянии l2 = 10 см, скорость атомов v=0.5 км/с. Определим расстояние b между компонентами расщепленного пучка на экране.
Заполненные оболочки дают нулевой вклад в магнитный момент атома. Атом серебра имеет один валентный электрон (в основном состоянии l=0) и потому его магнитный момент равен собственному магнитному моменту электрона. В неоднородном поле на атом действует сила

где mB — магнетон Бора. Знаки + соответствуют двум возможным направлениям магнитного момента электрона, и потому пучок расщепляется на два. На экране наблюдаются две полоски, находящиеся на расстоянии b друг от друга. Если в формулу (5.16) подставить выражение для силы Fz, то получим два отклонения s, отличающиеся знаком. Поэтому искомое расщепление b=2s. В результате приходим к выражению
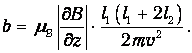
| (5.17) |
Массу атома серебра легко найти по таблице Менделеева: молярная (атомная) масса М=107.868 г/моль. Чтобы найти массу атома, надо молярную массу М разделить на число Авогадро:

Подставим теперь в (5.17) численные значения:

Такое расщепление вполне наблюдаемо в опытах.
Поиск по сайту:


