Соотношения неопределенностей. Само наличие у частицы волновых свойств накладывает определенные ограничения на возможность корпускулярного описания ее поведения

Само наличие у частицы волновых свойств накладывает определенные ограничения на возможность корпускулярного описания ее поведения. Для классической частицы всегда можно указать ее точное положение и импульс. Для квантового объекта имеем иную ситуацию.

Представим цуг волн пространственной протяженностью Dх - образ локализованного электрона, положение которого известно с точностью Dх. Длину волны де Бройля для электрона можно определить, подсчитав число N пространственных периодов на отрезке Dх:

Какова точность определения l? Ясно, что для слегка отличающейся длины волны мы получим примерно то же самое значение N. Неопределенность Dl в длине волны ведет к неопределенности

в числе узлов, причем измерению доступны лишь DN>1. Так как

то отсюда немедленно следует знаменитое соотношение неопределенностей В. Гейзенберга для координат-импульсов (1927 г.):

Точности ради надо заметить, что, во-первых, величина р в данном случае означает проекцию импульса на ось х и, во-вторых, приведенное рассуждение имеет скорее качественный, нежели количественный характер, поскольку мы не дали строгой математической формулировки, что понимается под неопределенностью измерения. Обычно соотношение неопределенностей для координат-импульсов записывается в виде

(3.12)

Аналогичные соотношения справедливы для проекций радиуса-вектора и импульса частицы на две другие координатные оси:

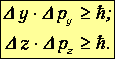
Представим теперь, что мы стоим на месте и мимо проходит электронная волна. Наблюдая за ней в течение времени Dt, хотим найти ее частоту n. Насчитав N = Dtn колебаний, определяем частоту с точностью

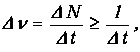
откуда имеем

или (с учетом соотношения Е=hv)

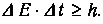
Аналогично неравенству (3.12) соотношение неопределенностей Гейзенберга для энергии системы чаще используется в виде

(3.13)

Поговорим о физическом смысле этих соотношений. В них проявляется «несовершенство» макроскопических приборов. Но приборы совсем не виноваты: ограничения носят принципиальный, а не технический характер. Сам микрообъект не может быть в таком состоянии, когда определенные значения одновременно имеют какая-то из его координат и проекция импульса на ту же ось.

Смысл второго соотношения: если микрообъект живет конечное время, то его энергия не имеет точного значения, она как бы размыта. Естественная ширина спектральных липни - прямое следствие формул Гейзенберга. На стационарной орбите электрон живет неограниченно долго и энергия Е определена точно. В этом - физический смысл понятия стационарного состояния. Если неопределенность в энергии электрона превышает величину расщепления между энергиями соседних состояний

то нельзя точно сказать, на каком уровне находится электрон. Иными словами, на короткое время порядка

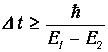
электрон может перескочить с уровня 1 на уровень 2, не излучая фотона, и затем вернуться назад. Это - виртуальный процесс, который не наблюдается и, следовательно, не нарушает закона сохранения энергии.

Похожие соотношения существуют и для других пар так называемых сопряженных динамических переменных. Так, при вращении частицы вокруг некоторой оси по орбите радиусом R неопределенность ее угловой координаты Dj влечет за собой неопределенность ее положения на орбите Dх=RDj. Из соотношений (3.12) следует, что неопределенность импульса частицы удовлетворяет неравенству

Учитывая связь момента импульса электрона L с его импульсом L=Rp, получаем DL=RDp, откуда следует еще одно соотношение неопределенностей

Поиск по сайту: