АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Безусловные вероятности состояний марковской цепи

Читайте также:
  1. Алгоритм моделирования по принципу особых состояний.
  2. Анализ вероятности
  3. Анализ психических состояний у занимающихся йогой по методике Айзенка
  4. Аналитическая деятельность командира по анализу и оценке морально-психологических состояний военнослужащих
  5. Безусловные переходы
  6. БЕЗУСЛОВНЫЕ РЕФЛЕКСЫ
  7. Вероятности начальных состояний цепи Маркова
  8. Вероятности перехода цепи Маркова
  9. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях
  10. вибрации и показателей вероятности вибрационной болезни
  11. Виды терминальный состояний

Кроме условных вероятностей (матриц перехода) часто возникает необходимость найти безусловные вероятности состояний системы в 1, 2,…, n -й моменты времени. Для их определения используют вектор-строку вероятностей начальных состояний .

Безусловная (абсолютная) вероятность того, что после первого шага цепь Маркова перейдет в состояние j определяется очевидным соотношением

. (6.10)

Совокупность безусловных вероятностей состояний 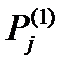образует вектор-строку .

Из (6.10) следует, что вектор-строка вероятностей состояния цепи после первого шага равняется произведению вектора-строки вероятностей начальных состояний на матрицу перехода, то есть

.

Очевидно, что вектор-строка вероятностей состояний после n -го шага определяется выражением

. (6.11)

Время существования процесса в поглощающей цепи Маркова конечно. Однако если в цепи отсутствуют поглощающие состояния, процесс в нем может развиваться как угодно долго. В связи с этим часто вызывает интерес вопрос о том, как с течением времени изменяются безусловные вероятности состояний эргодической ЦМ.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)