 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дискретные цепи Маркова (марковские цепи)
В теории вероятностей и во многих ее приложениях используется так называемая схема независимых испытаний. Значение термина "независимые испытания" заключается в том, что результат испытания в некоторый момент времени не влияет на результат любого другого испытания в любой следующий момент времени. Общая постановка задачи при этом такая: при заданных вероятностях каждой из возможных событий необходимо определить вероятность того, что за серию испытаний некоторое испытание состоится заданное количество раз. Такую задачу можно решать и для более сложного случая зависимых испытаний. В этом случае вероятность осуществления некоторого события в i -том испытании зависит от результатов 
предыдущих испытаний. При этом очевидно, предыдущие испытания по-разному влияют на результат испытания, которое осуществляется. Интуитивно можно считать, что при увеличении значения 
степень этого влияния уменьшается. Обычно величину 
ограничивают некоторым значением 
так, что при 
результаты испытаний уже не влияют на результат i -го испытания.
Последовательность таких зависимых испытаний называют цепью
Маркова.
Выбор значения величины m играет принципиальную роль, и определяет связность цепи.
ЦМ называется m-связной, если на результат каждого испытания влияют только m предыдущих испытаний.
Односвязную цепь (m =1) называют простой цепью Маркова (ПЦМ).
Роль теории ПЦМ настолько велика, что часто класс ЦМ ограничивается лишь односвязными ЦМ. Это обусловлено, в частности, тем, что марковские разрывные и непрерывные процессы определяются с помощью так называемого марковского свойства, которое в дискретном случае удовлетворяется лишь для простых цепей Маркова.
Марковское свойство определяется так: влияние испытания в момент времени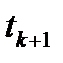 
зависит только от результата последнего испытания в момент времени 
и не зависит от результатов испытаний, проведенных до момента .
На промежуток времени между и 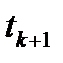никакие ограничения не накладываются. Важно лишь, чтобы эти моменты времени были фиксированы. Для упрощения анализа таких процессов чаще всего принимают 
.
Таким образом, ЦМ являются дискретными как по состоянию, так и по времени.
Для такого процесса моменты времени 
когда некоторая система S может изменять свое состояние, удобно рассматривать как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, рассматривать не время 
, а номер шага 
. Случайный процесс в этом случае характеризуется последовательностью состояний
, (6.1)
где 
– начальное состояние системы (перед первым шагом); 
– состояние системы непосредственно после первого шага и т. д.
Событие 
– система сразу после k -го шага находится в состоянии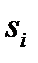 
является случайным событием и, следовательно, последовательность (6.1) можно рассматривать как последовательность случайных событий, причем эта последовательность образует ЦМ.
Рассмотрим пример.
Поиск по сайту: