 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема Маркова о предельных (финальных) вероятностях
Пусть есть некоторая эргодическая ЦМ. Тогда для нее справедлива такая теорема Маркова.
С увеличением количества шагов n вероятность перехода 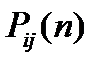 из состояния
из состояния 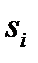 в состояние
в состояние 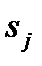 стремится к определенному пределу
стремится к определенному пределу 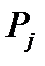 , который называется финальной вероятностью, то есть
, который называется финальной вероятностью, то есть
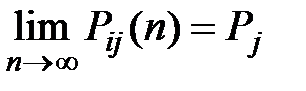 для всех i, j. (6.12)
для всех i, j. (6.12)
В матричной форме это записывается так:
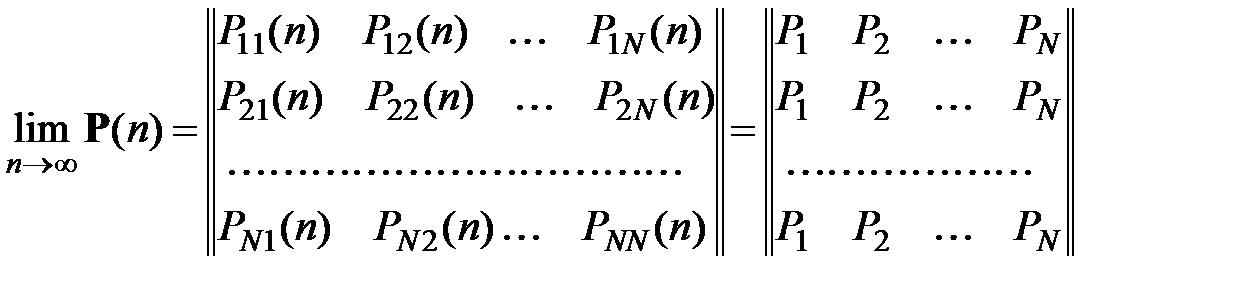 . (6.13)
. (6.13)
Из (6.12) и (6.13) вытекает, что предел вероятности перехода между любыми двумя состояниями эргодической цепи существует и не зависит от состояния 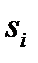 . Иначе говоря,
. Иначе говоря,
по прошествии длительного времени вероятность того, что процесс будет находиться в состоянии 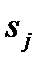 , не зависит от того, из какого состояния этот процесс начал развиваться. Поэтому говорят, что ЦМ "забывают" свое прошлое.
, не зависит от того, из какого состояния этот процесс начал развиваться. Поэтому говорят, что ЦМ "забывают" свое прошлое.
Кроме того, в эргодических цепях Маркова безусловные вероятности 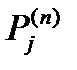 при увеличении n также стремятся к финальным вероятностям
при увеличении n также стремятся к финальным вероятностям 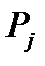 .
.
Режим работы эргодической ЦМ (системы) при достаточно большом значении n называют стационарным режимом ЦМ.
Вычисление финальных вероятностей при известных начальных вероятностях и заданной матрице перехода – важнейшая задача при изучении эргодических ЦМ. Для решения этой задачи можно использовать два алгоритма.
1) Воспользоваться теоремой Маркова, согласно которой возведение матрицы перехода в достаточно высокую степень n должно дать вектор-строку искомых вероятностей. Ясно, что этот алгоритм является чрезвычайно трудоемким.
2) Значительно проще найти эти вероятности решением системы алгебраических уравнений. Согласно формуле полной вероятности можно записать соотношение, справедливое при произвольном значении n
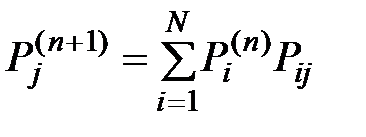 .
.
При больших значениях n безусловные вероятности равняются финальным вероятностям, поэтому
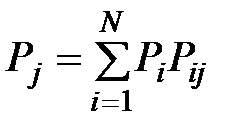 . (6.14)
. (6.14)
Получили систему N алгебраических уравнений с N неизвестными. Чтобы решить эту систему, из (6.14) надо взять N– 1 уравнение и дополнить систему условием нормировки 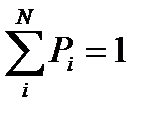 .
.
Рассмотрим еще два примера.
Первый пример.
В процессе эксплуатации ЭВМ можно рассматривать как некоторую физическую систему с 4-мя возможными состояниями: 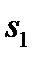 – ЭВМ полностью исправная;
– ЭВМ полностью исправная; 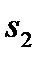 – ЭВМ имеет незначительные неисправности, но может решать задачи;
– ЭВМ имеет незначительные неисправности, но может решать задачи; 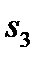 – ЭВМ имеет существенные неисправности и может решать лишь ограниченный класс задач;
– ЭВМ имеет существенные неисправности и может решать лишь ограниченный класс задач; 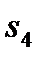 – ЭВМ полностью вышла из строя. Очевидно, что вместо ЭВМ таким же образом можно рассматривать и другие технические системы (приемные устройства, передающие устройства, каналы связи и др.). В начальный момент времени система полностью исправна. В фиксированные моменты времени
– ЭВМ полностью вышла из строя. Очевидно, что вместо ЭВМ таким же образом можно рассматривать и другие технические системы (приемные устройства, передающие устройства, каналы связи и др.). В начальный момент времени система полностью исправна. В фиксированные моменты времени 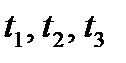 осуществляется проверка ЭВМ. Процесс, происходящий в системе, можно рассматривать как однородную цепь Маркова с тремя шагами, которые соответствуют трем проверкам. Матрица вероятностей перехода известна:
осуществляется проверка ЭВМ. Процесс, происходящий в системе, можно рассматривать как однородную цепь Маркова с тремя шагами, которые соответствуют трем проверкам. Матрица вероятностей перехода известна:
 .
.
Нужно найти вероятности состояний ЭВМ после трех проверок.
Решение:
Начнем с построения графа состояний. Граф приведено на рис. 6.3.
Очевидно, что вектор-строка вероятностей начальных состояний имеет вид 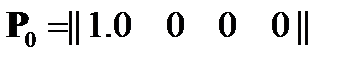 .
.
Находим вероятности состояний после первого шага:
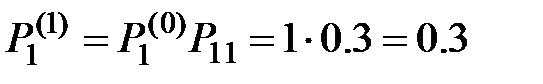 ;
; 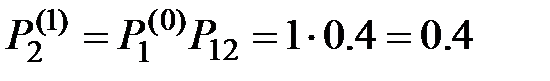 ;
;
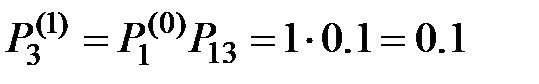 ;
; 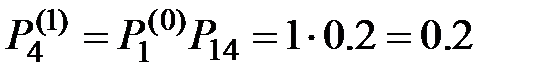 .
.
Вероятности состояний после второго шага:
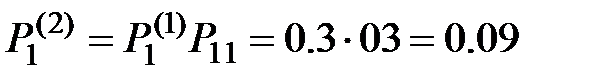 ;
;
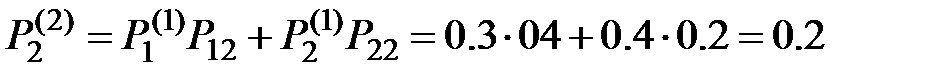 ;
;
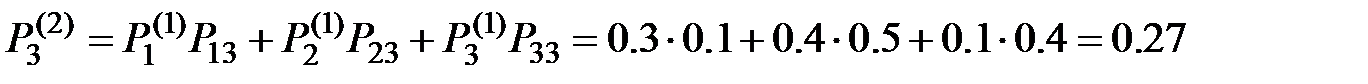 ;
;
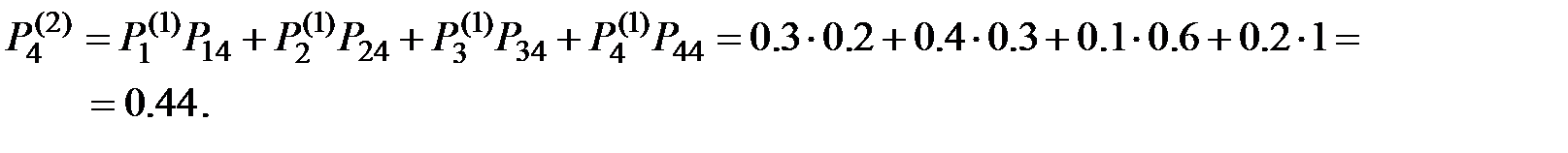
Наконец, искомые вероятности после третьего шага равняются:
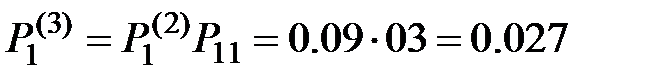 ;
;
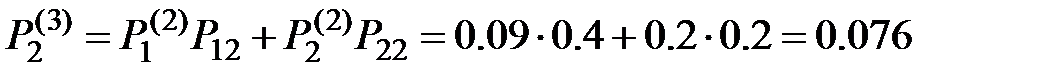 ;
;
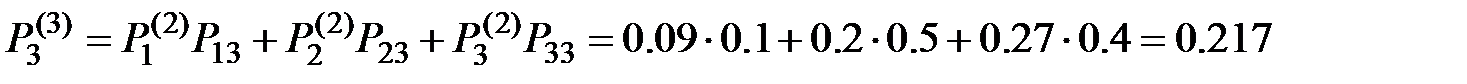 ;
;
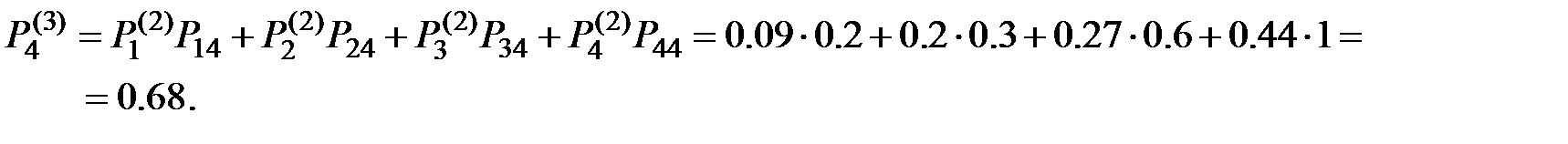 Проверим результат на выполнение условия нормировки:
Проверим результат на выполнение условия нормировки:
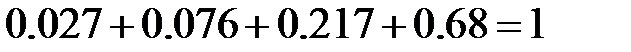 .
.
| Рис. 6. 3 |
Рассмотрим пример использования математического аппарата ЦМ для построения моделей речевых сигналов.
Второй пример.
Большинство звуков языка можно отнести или к вокализованным (гласным), или к невокализованным (согласным). Тогда речевой сигнал в системе связи можно представить как такой, что имеет три состояния: 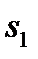 – пауза;
– пауза; 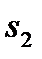 – вокализованный и
– вокализованный и 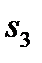 – невокализованный звуки. Необходимо построить модель языкового процесса с этими тремя состояниями на базе однородной ЦМ. Это значит, что надо найти финальные вероятности
– невокализованный звуки. Необходимо построить модель языкового процесса с этими тремя состояниями на базе однородной ЦМ. Это значит, что надо найти финальные вероятности 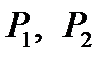 и
и 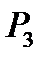 .
.
Решение:
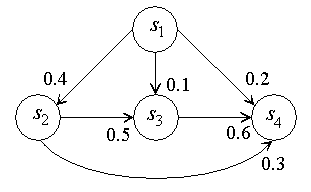
Начнем с построения ориентированного графа. Он изображен на рис. 6.4. Все возможны переходы из одного состояния в другой отмечены соответствующими дугами с указанием вероятности перехода. Если по некоторым причинам любые переходы в системе невозможны, это не изменит граф. Просто соответствующие вероятности перехода будут равняться нулю.
В случае, который рассматривается 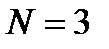 .
.
Запишем матрицу перехода однородной цепи Маркова для нашего случая.
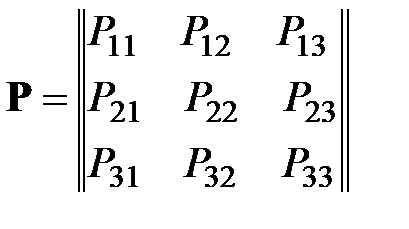 .
.
Чтобы найти финальные вероятности, воспользуемся алгоритмом 2). Для этого составим систему трех алгебраических уравнений с тремя неизвестными. Первые два уравнения получим из (6.14) и третье – из условия нормировки.
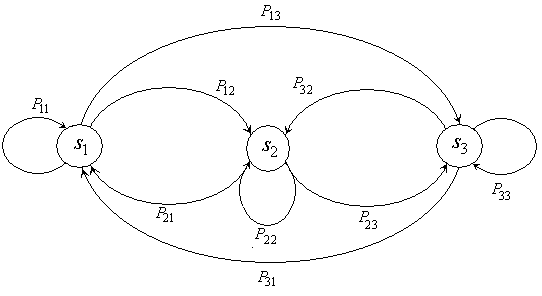
| Рис. 6. 4 |
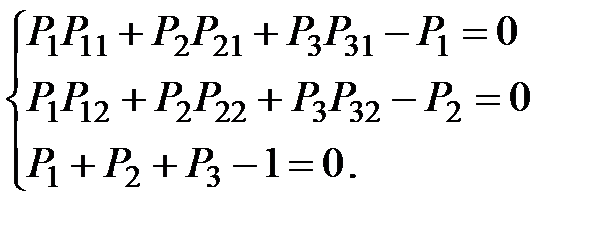
Осталось решить систему. Воспользуемся ЭВМ и системой MATHEMATICA. Ниже приведен оператор, с помощью которого решена эта система уравнений, и формулы для вычисления финальных вероятностей 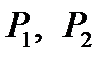 и
и 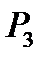 . Эти формулы полностью описывают модель исследуемого процесса с тремя состояниями.
. Эти формулы полностью описывают модель исследуемого процесса с тремя состояниями.
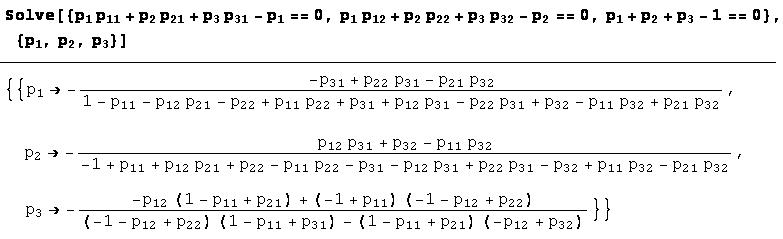
6.2. Канал связи – модель «черного ящика » [3, 4]
Динамическая система в технике обычно характеризуется своим функциональным назначением – усилитель, контроллер двигателя, радиопередающие и радиоприемные устройства, модемы, кодеки и т. д. Для физических систем, наблюдаемых в природе (например, в солнечной системе), достаточно ответить на вопрос «Как она действует?» В случае же технической системы необходимо также выяснить: «Для чего она предназначена?» Аналогичный интерес к целевому назначению возникает при изучении биологических систем и общественных формаций, которые, как обычно считается, развивались в условиях ограничений, породивших видимость целенаправленности.
Таким образом, при изучении технических систем приходится постоянно обращаться как к их функциональным описаниям (передаточная функция, «черный ящик»), так и к структурным (принципиальная или блочная схема, характеристика состояния). Переход от структурного к функциональному описанию требует анализа заданной структуры для определения ее передаточной характеристики. Обратный переход может потребоваться при синтезе структуры с заданной функциональной характеристикой.
Математически функциональное описание системы имеет вид оператора
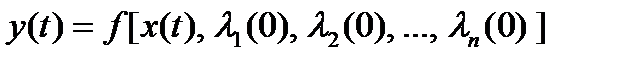 ,
,
где: х (t) входной сигнал; у (t) выходной сигнал (отклик системы на входное воздействие х (t)); 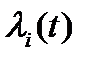 переменные состояния системы.
переменные состояния системы.
Системы, естественно, могут иметь более одного входа или выхода. В этом случае необходимо внести соответствующие формальные изменения в функциональное описание системы. Заметим, что система, характеризующаяся, например, функцией вида 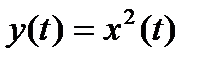 является более ограниченной, чем система, характеризующаяся оператором типа
является более ограниченной, чем система, характеризующаяся оператором типа 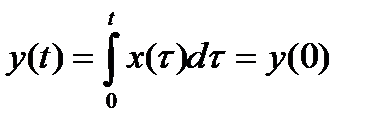 . В первом случае текущее значение выходного сигнала зависит лишь от текущего значения сигнала на входе, во втором случае величина выходного сигнала зависит от значений сигнала на входе в различные моменты времени, например в течение всего интервала от t = 0 до настоящего момента. Более того, наличие в выражении компонента у (0) свидетельствует о том, что в выходном сигнале учитываются даже более отдаленные воздействия [4].
. В первом случае текущее значение выходного сигнала зависит лишь от текущего значения сигнала на входе, во втором случае величина выходного сигнала зависит от значений сигнала на входе в различные моменты времени, например в течение всего интервала от t = 0 до настоящего момента. Более того, наличие в выражении компонента у (0) свидетельствует о том, что в выходном сигнале учитываются даже более отдаленные воздействия [4].
В качестве примера рассмотрим простой, но важный случай, а именно: система является линейной с постоянными параметрами, а входное воздействие – детерминированный сигнал [3].
Для решения этой задачи чаще других применяют один из следующих трех методов:
● классический метод, основанный на решении дифференциального уравнения, моделирующего процессы, происходящие в системе при действии на нее заданного сигнала;
● метод интеграла свертки, позволяющий находить отклик системы непосредственно во временной области;
● спектральный метод, позволяющий найти отклик системы в частотной области.
При решении инженерных и научных задач радиотехники и связи в основном используется третий из перечисленных методов.
В качестве системы может выступать как собственно линейная система с постоянными параметрами, так и канал связи.
Вспомним особенности анализа линейной системы с постоянными параметрами во временной области. Потом более детально рассмотриманализ в частотной области и сформулируем алгоритмы анализа и синтеза таких систем.
Поиск по сайту: