 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение Колмогорова - Чепмена
Для однородной цепи Маркова вероятность перехода из i -го в j- ое состояние за 2 шага, то есть  , определяется таким очевидным соотношением:
, определяется таким очевидным соотношением:
 , (6.5)
, (6.5)
где 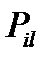 и
и  – элементы заданной матрицы перехода за 1 шаг.
– элементы заданной матрицы перехода за 1 шаг.
Переходя к матричной записи выражения (6.5), получаем, что матрица перехода за 2 шага равняется произведению двух одинаковых матриц (6.3), то есть
 . (6.6)
. (6.6)
Вероятность перехода из i -го в j- ое состояние за 3 шага можно вычислить по формуле
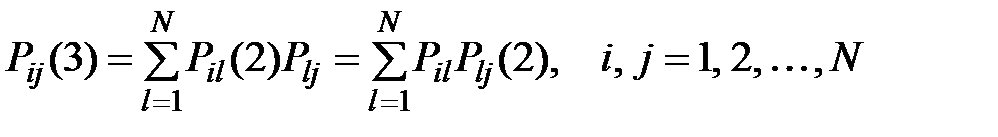
или
 .
.
В общем случае получаем
 . (6.7)
. (6.7)
Дальше, если анализировать вероятности перехода за п шагов, то как промежуточный момент можно выбрать любой  -й момент.
-й момент.  . Тогда, для вычисления вероятностей
. Тогда, для вычисления вероятностей  необходимо знать только матрицы перехода
необходимо знать только матрицы перехода  и
и  , то есть
, то есть
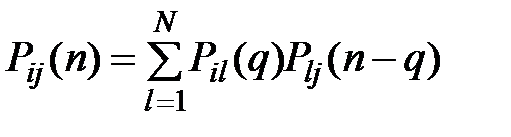 (6.8)
(6.8)
или
 . (6.9)
. (6.9)
Матрица перехода за n шагов равняется произведению матрицы перехода зa q шагов и матрицы перехода за  шагов.
шагов.
Соотношение (6.9) устанавливает связь между вероятностями перехода для любых трех последовательных моментов времени и носит название уравнения Колмогорова-Чепмена.
Поиск по сайту: