АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вероятности начальных состояний цепи Маркова

Читайте также:
  1. VII. Вопросник для анализа учителем особенностей индивидуального стиля своей педагогической деятельности (А.К. Маркова)
  2. Алгоритм моделирования по принципу особых состояний.
  3. Анализ вероятности
  4. Анализ психических состояний у занимающихся йогой по методике Айзенка
  5. Аналитическая деятельность командира по анализу и оценке морально-психологических состояний военнослужащих
  6. Безусловные вероятности состояний марковской цепи
  7. Вероятности перехода цепи Маркова
  8. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях
  9. вибрации и показателей вероятности вибрационной болезни
  10. Виды терминальный состояний
  11. Виды эмоциональных реакций (эмоции) и эмоциональных состояний

Вероятности перехода – это важнейшая характеристика любой ЦМ. Однако они по определению являются условными вероятностями. Чтобы полностью задать ЦМ, кроме матрицы перехода необходимо задать еще вероятности начальных состояний цепи – начальные условия.

 

Вероятности начальных состояний 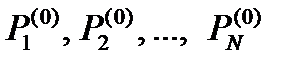являются безусловными вероятностями и образуют вектор-строку

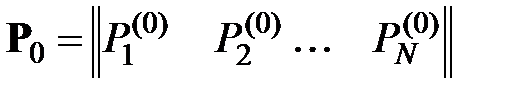, (6.4)

сумма элементов которого по условию нормировки должна равняться единице.

 

Если начальное состояние системы известно точно, например, это состояние 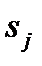, тогда 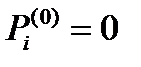для всех 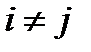и .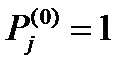

Следовательно, если известны матрица перехода (6.2) и вектор-строка вероятности начальных состояний (6.4), ЦМ полностью определена. Теперь можно начать анализ процессов, которые происходят в ЦМ. Рассмотрим сначала такую задачу.

Пусть некоторая система в данный момент времени находится в состоянии . Нужно найти вероятность того, что система перейдет в состояние за 2, 3, …, n шагов. Иначе говоря, нужно найти матрицу перехода для заданного количества шагов, если известна матрица перехода за 1 шаг.

 
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)