АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример 6.1

Читайте также:
  1. X. примерный перечень вопросов к итоговой аттестации
  2. Буду на работе с драконом примерно до 21:00.
  3. Булевы функции. Способы задания. Примеры.
  4. В некоторых странах, например в США, президента заменяет вице-
  5. В примере
  6. В странах Востока (на примере Индии и Китая)
  7. Вания. Одной из таких областей является, например, регулирова-
  8. Вашим сообщениям, например, спеть «С днем рождения»
  9. Виды знания. Контрпример стандартному пониманию знания
  10. Власть примера. Влияние с помощью харизмы
  11. Внешний долг (внешняя задолженность): пример России
  12. Вопрос 11. Герои романтических поэм М. Ю. Лермонтова (на примере одного произведения).

Пусть имеется ЦМ с N состояниями . Рассмотрим, что собой представляет МП во временной области.

Решение:

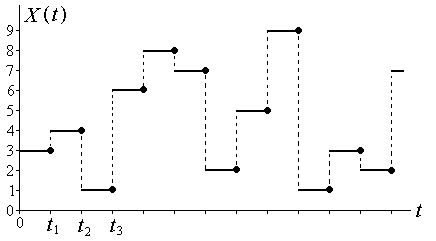
Рис. 6. 1

Обозначим 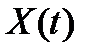номер состояния, в котором находится система 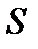в момент времени t. Тогда процесс (ЦМ) описывается целочисленной случайной функцией . Эта функция с какой-то вероятностью может принимать значения , осуществляя скачки от одного целого значения к другому в заданные моменты времени 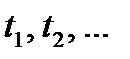. График одной из возможных реализаций этой функции приведен на рис. 6.1. Эта функция является непрерывной слева, что отмечено точками на рисунке.

Одномерный закон распределения мгновенных значений случайной функции 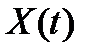(МП) определяется вероятностями того, что после k-го и до (k+1) шага система S будет находиться в состоянии 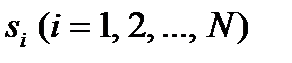. Эти вероятности называют вероятностями состояний цепи Маркова и их чаще всего и надо находить при решении конкретных задач, встречающихся на практике. Пока что мы можем утверждать одно, а именно:

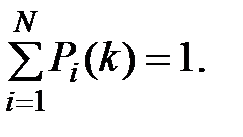
Ê

Как следует из рассмотренного примера и графика, приведенного на рис. 6.1, чтобы найти вероятности состояний ЦМ, необходимо знать вероятности переходов из одного состояния в другое и вероятности состояний в начале процесса.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)