 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дискретно-детерминированные модели (ДД-модели, F-схемы)
Особенности ДД-подхода на этапе формализации процесса функционирования систем заключается в том, что в качестве математического аппарата часто используется теория автоматов. На основе этой теории система представляется в виде автомата, который преобразует дискретную информацию и меняет внутренние состояния лишь в конкретные моменты времени. Автомат можно представить в виде некоторого устройства (черного ящика), на которое подаются входные сигналы и снимаются выходные и которые могут иметь некоторые внутренних состояний. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а, следовательно, и множество выходных сигналов), но это множество является конечным.
Абстрактно конечный автомат (finite automata) можно представить как математическую схему ( схему), которая характеризуется шестью элементами:
схему), которая характеризуется шестью элементами:
· конечным множеством  входных сигналов (входным алфавитом);
входных сигналов (входным алфавитом);
· конечным множеством  выходных сигналов (выходным алфавитом);
выходных сигналов (выходным алфавитом);
· конечным множеством  внутренних состояний (внутренним алфавитом или алфавитом состояний);
внутренних состояний (внутренним алфавитом или алфавитом состояний);
· начальным состоянием 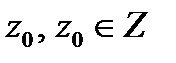 ;
;
· функцией переходов  ;
;
· функцией выходов  .
.
Автомат, который задается F -схемой, 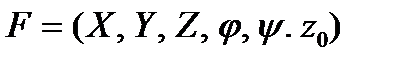 функционирует в дискретном автоматном времени, то есть по тактам, через одинаковые интервалы времени, примыкающими друг к другу. Каждому из них соответствуют постоянные значения входного и выходного сигналов и внутренних состояний.
функционирует в дискретном автоматном времени, то есть по тактам, через одинаковые интервалы времени, примыкающими друг к другу. Каждому из них соответствуют постоянные значения входного и выходного сигналов и внутренних состояний.
Понятие  -автомат в ДД-подходе к исследованию на моделях свойств объектов является математической абстракцией, удобной для описания широкого класса процессов функционирования реальных объектов в автоматизированных системах обработки информации и управления. Такими объектами в первую очередь являются элементы и узлы ЭВМ, устройства контроля, регулирования и управления, системы временной и пространственной коммутации в технике обмена информацией и так далее. Для всех перечисленных объектов характерно наличие дискретных состояний и дискретный характер работы во времени, и их описание с помощью F- схем является эффективным.
-автомат в ДД-подходе к исследованию на моделях свойств объектов является математической абстракцией, удобной для описания широкого класса процессов функционирования реальных объектов в автоматизированных системах обработки информации и управления. Такими объектами в первую очередь являются элементы и узлы ЭВМ, устройства контроля, регулирования и управления, системы временной и пространственной коммутации в технике обмена информацией и так далее. Для всех перечисленных объектов характерно наличие дискретных состояний и дискретный характер работы во времени, и их описание с помощью F- схем является эффективным.
Дискретно-стохастические модели (ДС-модели, Р-схемы)
Кратко рассмотрим особенности построения ММ (схем) при ДС-подходе к формализации процесса функционирования исследуемой системы  . Поскольку суть дискретизации времени при этом подходе остается аналогичной рассмотренным конечным автоматам, то влияние фактора стохастичности можно проследить на разновидности таких автоматов, а именно на вероятностных (стохастических) автоматах.
. Поскольку суть дискретизации времени при этом подходе остается аналогичной рассмотренным конечным автоматам, то влияние фактора стохастичности можно проследить на разновидности таких автоматов, а именно на вероятностных (стохастических) автоматах.
В общем виде вероятностный автомат можно определить как дискретный потактовый преобразователь информации с памятью, функционирование которого в каждом такте зависит лишь от состояния памяти в нем и может быть описано статистически.
Использование схем вероятностных автоматов важно при разработке методов проектирования дискретных систем, в которых присутствует статистически закономерное случайное поведение, а также для выяснения алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, для решения задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.
Уточним математическое понятие Р -автомата, используя понятия, введенные для F -автомата. Введем множество G, элементами которого являются всевозможные пары  , где
, где  и
и  – элементы входного подмножества Х и подмножества состояний Z соответственно. Если существуют две такие функции
– элементы входного подмножества Х и подмножества состояний Z соответственно. Если существуют две такие функции  и
и  , с помощью которых осуществляются отображения
, с помощью которых осуществляются отображения  и
и  , то говорят, что
, то говорят, что  определяет автомат детерминированного типа.
определяет автомат детерминированного типа.
Теперь можно рассмотреть общую математическую схему. Пусть Ф – множество всевозможных пар вида  , где
, где  – элемент выходного подмножества
– элемент выходного подмножества  . Потребуем, чтобы любой элемент множества G порождал на множестве Ф некоторый закон распределения следующего вида:
. Потребуем, чтобы любой элемент множества G порождал на множестве Ф некоторый закон распределения следующего вида:
Элементы из Ф … 

При этом
 ,
,
где  – вероятность перехода системы (автомата) в состояние
– вероятность перехода системы (автомата) в состояние  и появления на выходе сигнала
и появления на выходе сигнала  , если он был в состоянии
, если он был в состоянии  и на его вход в этот момент времени поступил сигнал
и на его вход в этот момент времени поступил сигнал 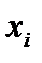 . Количество таких распределений, представленных в виде таблиц, равняется числу элементов множества G. Обозначим множество этих таблиц В. Тогда четверка элементов
. Количество таких распределений, представленных в виде таблиц, равняется числу элементов множества G. Обозначим множество этих таблиц В. Тогда четверка элементов 
называется вероятностным автоматом (Р -автоматом).
Для оценки разных характеристик исследуемых систем, представляемых в виде Р -схем, наряду с аналитическими моделями можно применять и имитационные модели, которые реализуются, например, методом статистического моделирования.
Поиск по сайту: