АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Классификация состояний и цепей Маркова

Читайте также:
  1. IX.4. Классификация наук
  2. MxA классификация
  3. VII. Вопросник для анализа учителем особенностей индивидуального стиля своей педагогической деятельности (А.К. Маркова)
  4. Аденовирусная инфекция. Этиология, патогенез, классификация, клиника фарингоконъюнктивальной лихорадки. Диагностика, лечение.
  5. Акустические колебания, их классификация, характеристики, вредное влияние на организм человека, нормирование.
  6. Алгоритм моделирования по принципу особых состояний.
  7. Анализ психических состояний у занимающихся йогой по методике Айзенка
  8. Аналитическая деятельность командира по анализу и оценке морально-психологических состояний военнослужащих
  9. Аналитические методы при принятии УР, основные аналитические процедуры, признаки классификации методов анализа, классификация по функциональному признаку.
  10. Атомные нарушения структуры кристалла. Классификация дефектов структуры.
  11. Аюрведическая классификация болезней
  12. Безопасность технологического оборудования: классификация, требования безопасности и основные направления обеспечения безопасности

● Состояние называют необратимым, если существует такое состояние и такое количество шагов , что , но 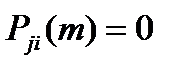для всех значений m. Остальные состояния называются обратимыми.

● Два состояния и , для которых и , то такие состояния называются соединеняющимися.

● Если соединяется с , а состояние соединяется с , то состояние соединяется с . Это свойство состояний цепи Маркова позволяет множество обратимых состояний разбить на классы (подмножества) соединяющихся состояний так, что состояния, которые принадлежат разным классам, не соединяются между собой.

● Если множество соединяющихся состояний состоит из одного состояния, это состояние называется поглощающим состоянием. В это состояние процесс может войти, но выйти из него не может. Это значит, что для поглощающего состояния вероятности перехода равняются: , а .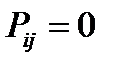

● Если среди всех состояний МЦ есть хотя бы одно поглощающее состояние, цепь называют поглощающей цепью Маркова.

● ЦМ, которая не содержит поглощающих состояний и состоит из одного класса соединеняющихся состояний, называют эргодической ЦМ.

Рис. 6. 2
На практике удобно изображать ЦМ в виде ориентированного графа, позволяющего наглядно представить возможный характер развития процесса. Вершины графа соответствуют состояниям цепи. Каждой дуге перехода из состояния в состояние ставится в соответствие вероятность перехода . Пример ориентированного графа ЦМ приведен на рис. 6.2.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)