АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях

Читайте также:
  1. Cоздание массивов постоянной длины
  2. а) Находим границы, в которых с вероятностью 0,9946 заключено среднее время обслуживания всех клиентов пенсионного фонда.
  3. Алгоритм изменения дозы НФГ в зависимости от относительной величины АЧТВ (по отношению к контрольной величине конкретной лаборатории)
  4. Анализ вероятности
  5. Атомный стандарт частоты
  6. Б. Договор постоянной ренты
  7. Безусловные вероятности состояний марковской цепи
  8. Блочная фототриангуляция по методу независимых маршрутов
  9. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
  10. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
  11. В таблице показана зависимость частоты генерированного переменного тока от количества магнитных полюсов и числа оборотов генератора
  12. Вероятности начальных состояний цепи Маркова

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна . Найдем вероятность того, что отклонение относительной частоты от постоянной вероятности p по абсолютной величине не превышает заданного числа . Другими словами, найдем вероятность осуществления неравенства

(4.9)

Эту вероятность будем обозначать так: . Заменим неравенство (4.9) ему равносильными или . Умножая эти неравенства на положительный множитель , получим неравенства, равносильные исходному:

.

Воспользуемся интегральной теоремой Лапласа. Обозначим через .

.

Окончательно:

(4.10)

Итак, вероятность осуществления неравенства приближенно равна значению удвоенной функции Лапласа при .

Пример 4.5. Вероятность того, что деталь не стандартна p= 0,1. найти, сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544 можно было утверждать, что относительная частота появления нестандартных деталей отклонится от постоянной вероятности p по абсолютной величине не более чем на 0,03.

Решение. ; ; . Найти n.

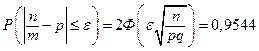
, . По таблице находим, что . Следовательно, ; ; .

 


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)