Формула Бернулли

ЛЕКЦИЯ № 4

ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ

План

1. Формула Бернулли

2. Локальная теорема Лапласа

3. Интегральная теорема Лапласа

4. Формула Пуассона

5. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях

Формула Бернулли

Практические задачи, связанные с оценкой вероятности наступления события в результате нескольких равноценных попыток могут анализироваться с применением формулы Бернулли или (при большом количестве таких попыток) с применением приближенной формулы Пуассона.

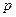Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события одна и та же и равна . Испытания предполагаются независимыми (т.е. считается, что вероятность появления события в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события обычно называют успехом, а не наступление – неудачей. Обозначим вероятность неудачи .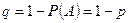

Вероятность события, заключающееся в том, что в 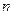испытаниях событие наступит раз и не наступит 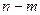раз, по теореме умножения вероятностей независимых событий равна . Таких сложных событий может быть столько, сколько можно составить сочетаний из 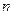элементов по элементов, т.е. 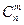. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятность всех сложных событий одинакова, то вероятность того, что в 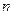независимых испытаниях успех наступит ровно раз, выражается формулой Бернулли:

(4.1)

Вероятность 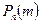при данном 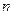сначала увеличивается при увеличении от 0 до некоторого значения , а затем уменьшается при изменении от до 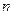. Поэтому , называют наивероятнейшим числом наступлений успеха в опытах. Это число , заключено между числами:

(4.2)

Если число – целое число, то наивероятнейших чисел два: 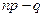и .

Пример 4.1. Определить вероятность того, что в семье, состоящей из пяти детей, будет 3 мальчика и 2 девочки. Рождение девочки и мальчика считать равновероятным.

Решение:

Будем считать, что событие состоит в появлении мальчика. Поскольку вероятность появления мальчика и девочки равны, то , . Согласно условию: , . Найдем число сочетаний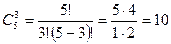

Согласно формуле Бернулли, искомая вероятность равна:

.

Поиск по сайту: