АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формула Пуассона

Читайте также:
  1. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  2. Адиабата Пуассона
  3. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  4. Барометрическая формула
  5. Барометрическая формула. Распределение Больцмана.
  6. Барометрическая формула. Распределение Больцмана.
  7. Барометрическая формула. Распределение Больцмана.
  8. Визначити енергію вибуху балону. Формула (3)
  9. Внешний фотоэффект и его законы. Формула Эйнштейна для фотоэффекта.
  10. Вопрос 2 Формула апостериорной вероятности Байеса
  11. Вопрос 2 Формула апостериорной вероятности Байеса.
  12. Вопрос 2 Формула апостериорной вероятности Байеса.

Если вероятность события p (или q) в отдельном испытании близка к нулю, то даже при большом числе испытаний 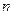, но небольшой величине произведения (меньше 10) вероятности , полученные по формуле (4.3) недостаточно близки к их истинным значениям. В таких случаях применяют другую асимптотическую формулу – формулу Пуассона, справедливость которой доказывается следующей теоремой.

Теорема. 4.3. Если вероятность 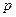наступления события в каждом испытании постоянна, но близка к нулю, число независимых испытаний 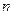достаточно велико, а произведение , то вероятность того, что в 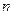независимых испытаниях событие наступит раз, приближенно равна:

(4.8)

(формула Пуассона).

Пример 4.4. Вероятность ДТП на данном участке дороги в течение суток равна 0,01. Найти вероятность того, что в течение 25 суток на данном участке произойдет одно ДТП.

Решение:

Поскольку условие выполняется, то нахождения вероятности воспользуемся формулой Пуассона:

.


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)