АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Интегральная теорема Лапласа

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Вектор индукции магнитного поля. Закон Био - Савара – Лапласа
  3. Внешние эффекты (экстерналии). Теорема Коуза.
  4. Внешние эффекты трансакционные издержки. Теорема Коуза
  5. Внешние эффекты, их виды и последствия. Теорема Коуза
  6. Внешние эффекты. Теорема Коуза.
  7. Внешние эффекты. Теорема Коуза.
  8. Вопрос 1 теорема сложения вероятностей
  9. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  10. Вопрос. Теорема Котельникова (Найквиста)
  11. Вопрос: Производная сложной функции. Производные и дифференциалы высших порядков. Теорема Ролля, Лагранжа, Коши.
  12. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.

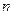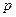Предположим, что проводится испытаний, в каждом из которых вероятность появления события постоянна и равна (). Вычислим вероятность того, что событие появится в 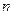испытаниях не менее раз и не более раз. Искомую вероятность можно найти с помощью интегральной теоремы Лапласа.

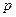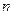Теорема 4.2. Если вероятность наступления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие в испытаниях от до раз, приближенно равна определенному интегралу:

(4.6)

где и . Функция Лапласа нечетная. При решении задач, требующих применение теоремы Лапласа, пользуются специальными таблицами, поскольку интеграл не выражается через элементарные функции. Формулу (4.6) можно записать следующим образом:

(4.7)

Функция Лапласа нечетная, т.е. .

Пример 4.3. Вероятность поражения мишени стрелком при одном выстреле равно 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена не менее 60 и не более 70 раз.

Решение:

Согласно условию , , , , . Воспользуемся интегральной теоремой Лапласа:

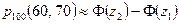
Найдем верхний и нижний пределы интегрирования:

,

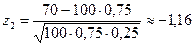
Искомая вероятность равна:

.


1 | 2 | 3 | 4 | 5 |

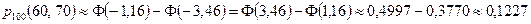Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)