Бернулли

Уравнение неразрывности струи. Рассмотрим течение идеальной жидкости внутри некоторой трубки тока, обладающей такими сечениями, что скорость молекул жидкости в любой точке каждого из них одинакова (см. рис. 14.4). Так как идеальная жидкость несжимаема, то ее масса, сосредоточенная между сечениями S1 и S2 трубки тока, с течением времени не изменяется. Следовательно, объемы жидкости dQ, протекшие через эти сечения за промежуток времени dt, будут равны. Поскольку dQ = S·u·dt, то выполняется соотношение:
S1·u1 = S2·u2 или
S·u = const. (14.4)
Выражение (14.4) называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости.

Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде

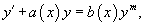
где a (x) и b (x) − непрерывные функции.

Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когда m = 1, уравнение преобразуется в уравнение с разделяющимися переменными.

В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки

Новое дифференциальное уравнение для функции z (x) имеет вид

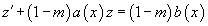
Поиск по сайту: