 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Затухающие колебания
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем наиболее часто встречающемся, случае сила сопротивления пропорциональна величине скорости:
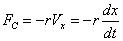 ,
,
где r – постоянная величина, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила и скорость имеют противоположные направления; следовательно, их проекции на ось X имеют разные знаки. Уравнение второго закона Ньютона при наличии сил сопротивления имеет вид:
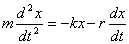 .
.
Применив обозначения 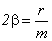 ,
,  , перепишем уравнение движения следующим образом:
, перепишем уравнение движения следующим образом:
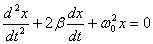 .
.
Это уравнение описывает затухающие колебания системы. Коэффициент  называется коэффициентом затухания.
называется коэффициентом затухания.

|
Экспериментальный график затухающих колебаний при малом коэффициенте затухания  представлен на рис. 7.6. Из рис. 7.6 видно, что график зависимости
представлен на рис. 7.6. Из рис. 7.6 видно, что график зависимости  выглядит как косинус, умноженный на некоторую функцию, которая убывает со временем. Эта функция представлена на рисунке штриховыми линиями. Простой функцией, которая ведет себя подобным образом, является экспоненциальная функция
выглядит как косинус, умноженный на некоторую функцию, которая убывает со временем. Эта функция представлена на рисунке штриховыми линиями. Простой функцией, которая ведет себя подобным образом, является экспоненциальная функция  . Поэтому решение можно записать в виде:
. Поэтому решение можно записать в виде:
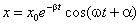 ,
,
где 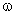 – частота затухающих колебаний.
– частота затухающих колебаний.
Величина x периодически проходит через нуль и бесконечное число раз достигает максимума и минимума. Промежуток времени между двумя последовательными прохождениями 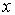 через нуль равен
через нуль равен 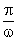 . Удвоенное его значение
. Удвоенное его значение 
 называется периодом колебаний.
называется периодом колебаний.
Множитель 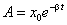 , стоящий перед периодической функцией
, стоящий перед периодической функцией  , называется амплитудой затухающих колебаний. Она экспоненциально убывает со временем. Скорость затухания определяется величиной
, называется амплитудой затухающих колебаний. Она экспоненциально убывает со временем. Скорость затухания определяется величиной 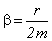 . Время, по истечении которого амплитуда колебаний уменьшается в
. Время, по истечении которого амплитуда колебаний уменьшается в  раз, называется временем затухания
раз, называется временем затухания  . За это время система совершает
. За это время система совершает  колебаний. Затухание колебаний принято характеризовать логарифмическим декрементом затухания. Логарифмическим декрементом затухания называется логарифм отношения амплитуд в моменты последовательных прохождений колеблющейся величины через максимум или минимум:
колебаний. Затухание колебаний принято характеризовать логарифмическим декрементом затухания. Логарифмическим декрементом затухания называется логарифм отношения амплитуд в моменты последовательных прохождений колеблющейся величины через максимум или минимум:
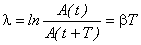 .
.
Он связан с числом колебаний  соотношением:
соотношением:
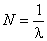 .
.
Величина  называется добротностью колебательной системы. Добротность тем выше, чем большее число колебаний успевает совершить система прежде, чем амплитуда уменьшится в
называется добротностью колебательной системы. Добротность тем выше, чем большее число колебаний успевает совершить система прежде, чем амплитуда уменьшится в 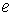 раз.
раз.
Постоянные величины  и
и 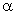 , как и в случае гармонических колебаний, можно определить из начальных условий.
, как и в случае гармонических колебаний, можно определить из начальных условий.
Поиск по сайту: