АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Кинетическая энергия тела при плоском движении

Читайте также:
  1. V2: Работа и энергия
  2. V2: Энергия волны
  3. Абсолютно упругий и неупругий удар тел. Внутренняя энергия. Общефизический закон сохранения энергии
  4. В схеме, состоящей из конденсатора и катушки, происходят свободные электромагнитные колебания. Энергия конденсатора в произвольный момент времени t определяется выражением
  5. Внутренняя энергия идеального газа
  6. Внутренняя энергия идеального газа. Работа газа при изобарном расширении. Применение первого начала термодинамики к изопроцессам. Понятие о втором начале термодинамики.
  7. Внутренняя энергия реального газа
  8. Внутренняя энергия реального газа. Эффект Джоуля - Томсона
  9. Внутренняя энергия тела и способы её изменения. Изменение внутренней энергии тела при нагревании. Первое начало термодинамики. Обратимые и необратимые процессы.
  10. Внутренняя энергия. Количество теплоты. Работа в термодинамике
  11. Вопрос 29 Энергия электростатического поля
  12. Вопрос 42 Энергия магнитного поля тока

Плоским (плоскопараллельным) называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Представим плоское движение тела как поступательное движение со скоростью 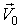, некоторой точки 0 в нем и вращения вокруг оси, проходящей через эту же точку и перпендикулярной 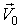с угловой скоростью .

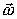В этом случае скорость i -той материальной точки тела определяется формулой

.

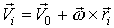Кинетическая энергия i - той материальной точки равна

или

.

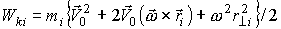Просуммировав по всем материальным точкам, получим

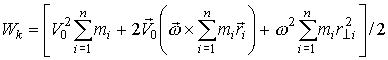
или 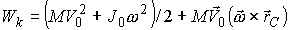, (12)

где М - полная масса тела, 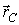- радиус-вектор центра масс, - момент инерции тела относительно оси, проходящей через точку О.

Если в качестве точки О взять центр масс тела С, то 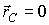и формула (12) упрощается: 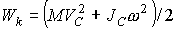. (13)

Таким образом, если разбить плоское движение тела на поступательное со

скоростью центра масс V c и вращательное с угловой скоростью w вокруг оси, проходящей через центр масс тела, то кинетическая энергия распадается на два независимых слагаемых, одно из которых определяется только скоростью центра масс V c, а другое - угловой скоростью w.

Из (13) следует, что при вращении тела относительно оси z, проходящей через центр масс С, его кинетическая энергия . (14)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)