Естественный способ описания движения. Тангенциальное и нормальное ускорения

Он обычно используется, если известна траектория движения точки.

При этом начало отсчета берется на траектории, также выбирается положительное направление движения вдоль траектории, а положение частицы описывается криволинейной координатой l(t), представляющей длину дуги кривой линии, отсчитанной вдоль траектории от начальной точки O -- иначе говоря, путь. В этом случае l = l(t) -- кинематическое уравнение движения.

Свяжем с траекторией естественную систему координат, состоящую из трех взаимно-перпендикулярных осей: касательной (единичный вектор ), нормали (единичный вектор ) и бинормали (единичный вектор ), составляющей правый винт с касательной и нормалью.

Тогда .Ускорение частицы .
Первое слагаемое направлено по касательной к траектории и называется тангенциальным (касательным) ускорением: . Модуль его равен производной от величины скорости по времени, поэтому тангенциальное ускорение характеризует изменение скорости по величине. Второе слагаемое в формуле направлено по нормали к траектории, характеризует изменение скорости по направлению, называется нормальным ускорением и определяется
выражением: . Его модуль 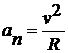. Заметим, что в случае движения частицы по окружности -- это хорошо известное центростремительное ускорение.

Итак, полное ускорение можно разложить на две составляющие:
тангенциальное ускорение и нормальное ускорение : , причем модуль полного ускорения .

Поиск по сайту: