Явления на границе жидкости и твердого тела

Форма поверхности жидкости, налитой в сосуд, определяется тремя факторами: силами взаимодействия между молекулами жидкости, силами взаимодействия между молекулами жидкости и молекулами, входящими в состав стенок сосуда, и действием силы тяжести.

Если достаточно большое количество жидкости налито в широкий сосуд, то жидкость вследствие преобладающего действия силы тяжести в этом случае имеет плоскую горизонтальную поверхность. Однако непосредственно у стенок сосуда поверхность жидкости несколько искривлена. Если молекулы жидкости, соприкасающиеся со стенкой сосуда, взаимодействуют с молекулами твердого тела сильнее, чем между собой, в этом случае жидкость стремится увеличить площадь соприкосновения с твердым телом. При этом поверхность жидкости изгибается вниз и говорят, что она смачивает стенки сосуда, в котором находится.

Если же молекулы жидкости взаимодействуют между собой сильнее, чем с молекулами стенок сосуда, то жидкость стремится сократить площадь соприкосновения с твердым телом, ее поверхность искривляется вверх, имеет место несмачивание жидкостью стенок сосуда.

Рис. 6.13

В узких трубочках, диаметр которых составляет доли миллиметра, искривленные края жидкости охватывают весь поверхностный слой, и вся поверхность жидкости в таких трубочках имеет вид, напоминающий полусферу. Это так называемый мениск. Он может быть вогнутым, как на рис. 6.13а, в случае смачивания, и выпуклым, как на рис. 6.13б, при несмачивании. Радиус кривизны поверхности жидкости при этом того же порядка, что и радиус трубки. Явления смачивания и несмачивания характеризуются краевым углом θ между смоченной поверхностью твердого тела и мениском в точках их соприкосновения (рис. 6.13а, б).

Наличие сил поверхностного натяжения и кривизны поверхности жидкости в капиллярной трубочке ответственно за дополнительное давление под искривленной поверхностью, называемое давлением Лапласа.

Рис. 6.14

Для вывода формулы, определяющей величину давления Лапласа, рассмотрим случай, когда поверхность жидкости в сосуде принимает форму выпуклого мениска (рис. 6.14). Пусть – сила поверхностного натяжения, действующая по касательной к поверхности жидкости, R – радиус кривизны поверхности мениска, r – радиус кривизны сечения мениска горизонтальной плоскостью. Силу можно разложить на две составляющие и 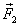. Очевидно, что при суммировании по периметру мениска все составляющие дадут ноль, и давление Лапласа будет обусловлено суммарным действием составляющих 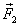. Найдем составляющую 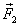и проведем суммирование по контуру, ограничивающему мениск в горизонтальном сечении, имея в виду, что сила поверхностного натяжения 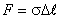, где Δ l – элемент длины контура.

,

(6.17)

.

(6.18)

Действие этой силы приходится на круговое сечение мениска площадью (рис. 6.14). Следовательно, избыточное давление Лапласа, обусловленное кривизной поверхности и действием сил поверхностного натяжения, равно

.

(6.19)

Можно обобщить полученную формулу на случай более сложной поверхности. В общем случае давление Лапласа определяется соотношением

,

(6.20)

где R ₁ и R ₂ – радиусы кривизны двух взаимно перпендикулярных сечений мениска.

Рис. 6.15

Радиусы кривизны, входящие в последнюю формулу, являются алгебраическими величинами. Если центр кривизны нормального сечения мениска находится под его поверхностью, то соответствующий радиус кривизны является положительной величиной (рис. 6.15а). В случае, когда центр кривизны находится над поверхностью мениска, R – отрицательно (рис. 6.15б). Отсюда следует, что под выпуклой поверхностью мениска давление Лапласа положительно (оно добавляется к атмосферному давлению Р ₀), под вогнутой поверхностью мениска давление Лапласа отрицательно (оно меньше атмосферного давления Р ₀ на величину Р _Л). Очевидно, что давление Лапласа тем больше, чем меньше радиус кривизны сечения, поэтому оно играет наиболее важную роль в капиллярных явлениях.

Применяя формулу Лапласа для частного случая сферической капли 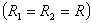, находим:

.

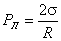(6.21)

Если поверхность мениска имеет цилиндрическую форму, то один из радиусов кривизны сечения можно считать равным бесконечности. Для этого частного случая давление Лапласа равно

.

(6.22)

В случае мыльного пузырька дополнительное давление, которое испытывает находящийся внутри него газ, равно , так как у пузырька две поверхности – наружная и внутренняя, каждая из которых создает дополнительное давление Лапласа.

Убедительной иллюстрацией существования лапласовского давления служит описанный ниже опыт.

Рис. 6.16

С помощью двух сообщающихся трубочек выдуваются мыльные пузыри (рис. 6.16), после этого трубочка С закрывается. Вследствие неизбежных случайных обстоятельств радиусы пузырей будут отличаться друг от друга. Внутри пузырька меньшего радиуса давление Лапласа больше, и воздух из него начнет перемещаться в пузырек большего радиуса. В результате большой пузырек будет увеличиваться в размерах, а маленький спустя непродолжительное время исчезнет

Поиск по сайту: