 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Фундаментальный смысл закона
| Симметрия в физике | ||
| Преобразование | Соответствующая инвариантность | Соответствующий закон сохранения |
| ↕ Трансляции времени | Однородность времени | …энергии |
| ⊠ C, P, CP и T-симметрии | Изотропность времени | …чётности |
| ↔ Трансляции пространства | Однородность пространства | …импульса |
| ↺ Вращения пространства | Изотропность пространства | …момента импульса |
| ⇆ Группа Лоренца | Относительность Лоренц-инвариантность | …4-импульса |
| ~ Калибровочное преобразование | Калибровочная инвариантность | …заряда |
Фундаментальный смысл закона сохранения энергии раскрывается теоремой Нётер. Согласно этой теореме, каждый закон сохранения однозначно соответствует той или иной симметрииуравнений, описывающих физическую систему. В частности, закон сохранения энергии эквивалентен однородности времени, то есть независимости всех законов, описывающих систему, от момента времени, в который система рассматривается.
Вывод этого утверждения может быть произведён, например, на основе лагранжева формализма[1]. Если время однородно, то функция Лагранжа, описывающая систему, не зависит явно от времени, поэтому полная её производная по времени имеет вид:
Здесь 
— функция Лагранжа, 
— обобщённые координаты и их первые и вторые производные по времени соответственно. Воспользовавшись уравнениями Лагранжа, заменим производные 
на выражение 
:
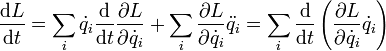
Перепишем последнее выражение в виде
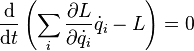
Сумма, стоящая в скобках, по определению называется энергией системы и в силу равенства нулю полной производной от неё по времени она является интегралом движения (то есть сохраняется).
Поиск по сайту: