Определение. Пусть имеются две системы отсчёта, одна из которых инерциальная, а другая ( ) движется относительно первой произвольным образом и в общем случае является

Пусть имеются две системы отсчёта, одна из которых инерциальная, а другая () движется относительно первой произвольным образом и в общем случае является неинерциальной. Будем также рассматривать движение произвольной материальной точки массы . Её ускорение по отношению к первой системе отсчёта обозначим , а по отношению ко второй — .

Связь между ускорениями и следует из теоремы Кориолиса (см. ниже):

где 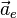— перено́сное ускорение, а — ускорение Кориолиса (кориолисово ускорение, поворотное ускорение). Напомним, что переносным ускорением называют ускорение той точки системы относительно системы , в которой в данный момент находится рассматриваемая материальная точка^[5].

После умножения на массу точки и учёта второго закона Ньютона , данное соотношение можно представить в виде

Величину называют переносной силой инерции, а величину — силой Кориолиса (кориолисовой силой). Обозначив их 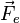и 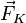соответственно, можно записать

Полученное выражение выражает основной закон динамики для неинерциальных систем отсчёта.

Из кинематики известно, что

где — угловая скорость вращения неинерциальной системы отсчёта , — скорость движения рассматриваемой материальной точки в этой системе отсчёта; квадратными скобками обозначена операция векторного произведения. С учётом этого для силы Кориолиса выполняется

Замечание. Следует иметь в виду, что в силу теоремы Кориолиса и принятой терминологии кориолисово ускорение материальной точки — это часть её ускорения в инерциальной системе отсчёта ^[6]. Поэтому было бы неправильно утверждать, что ускорение Кориолиса возникает в неинерциальной системе отсчёта . По тем же причинам, а также потому, что сила Кориолиса равна произведению массы точки на ускорение Кориолиса со знаком минус, неверным является утверждение о том, действие силы Кориолиса вызывает возникновение ускорения Кориолиса. В соответствии с общепринятой терминологией правильное утверждение заключается в том, что сила Кориолиса, действующая на материальную точку в системе отчёта , вызывает ускорение точки, равное ускорению Кориолиса, взятому со знаком минус.

Поиск по сайту: